题目内容
已知实数x,y满足方程x2+y2-4x+1=0.
(1)求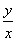 的最大值和最小值;
的最大值和最小值;
(2)求y-x的最大值和最小值;
(3)求x2+y2的最大值和最小值.
解 原方程可化为(x-2)2+y2=3,表示以(2,0)为圆心, 为半径的圆.
为半径的圆.
(1)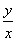 的几何意义是圆上一点与原点连线的斜率,
的几何意义是圆上一点与原点连线的斜率,
所以设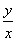 =k,即y=kx.
=k,即y=kx.
当直线y=kx与圆相切时,斜率k取最大值或最小值,此时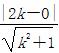 =
= ,解得k=±
,解得k=± (如图1).
(如图1).
所以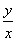 的最大值为
的最大值为 ,最小值为-
,最小值为- .
.

(2)y-x可看作是直线y=x+b在y轴上的截距,当直线y=x+b与圆相切时,
纵截距b取得最大值或最小值,此时 =
= ,解得b=-2±
,解得b=-2±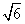 (如图2).
(如图2).
所以y-x的最大值为-2+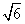 ,最小值为-2-
,最小值为-2-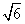 .
.
(3)x2+y2表示圆上的一点与原点距离的平方,由平面几何知识知,
在原点和圆心连线与圆的两个交点处取得最大值和最小值(如图3).
又圆心到原点的距离为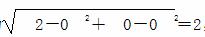
所以x2+y2的最大值是(2+ )2=7+4
)2=7+4 ,x2+y2的最小值是(2-
,x2+y2的最小值是(2- )2=7-4
)2=7-4 .
.

练习册系列答案
相关题目

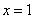 是函数
是函数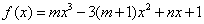 的一个极值点,其中
的一个极值点,其中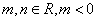 ,
,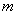 与
与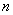 的关系式; (2)求
的关系式; (2)求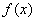 的单调区间;
的单调区间;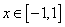 时,函数
时,函数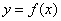 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3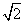 ,则m的倾斜角可以是:
,则m的倾斜角可以是: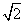 ,0)引直线l与曲线y=
,0)引直线l与曲线y=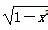 相交于A,B两点,O为坐标原点,当△AOB的面积取最大值时,直线l的斜率等于 ( ).
相交于A,B两点,O为坐标原点,当△AOB的面积取最大值时,直线l的斜率等于 ( ). A.
A.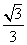 B.-
B.- -
- =1上的一点P到它的右焦点的距离为8,则点P到它的左焦点的距离是 ( ).
=1上的一点P到它的右焦点的距离为8,则点P到它的左焦点的距离是 ( ).