题目内容
同时掷两个骰子,两个骰子的点数和可能是2,3,4,…,11,12中的一个,事件A={2,5,7},事件B={2,4,6,8,10,12},那么A∪B={ },A∩
={ }.
. |
| B |
考点:互斥事件与对立事件
专题:集合
分析:根据集合的交并补的运算法则计算即可
解答:
解:∵事件A={2,5,7},事件B={2,4,6,8,10,12},
∴A∪B={2,4,5,6,7,8,10,12},
={3,5,7,9,11},
∴A∩
={5,7}
故答案为:{2,4,5,6,7,8,10,12},{5,7}
∴A∪B={2,4,5,6,7,8,10,12},
. |
| B |
∴A∩
. |
| B |
故答案为:{2,4,5,6,7,8,10,12},{5,7}
点评:本题考查了集合的交并补的法则,属于基础题

练习册系列答案
相关题目
甲通过英语考试的概率为
,乙通过英语考试的概率为
,甲乙两人同时通过英语考试的概率为
,则甲乙两人中至少有一人通过英语听力测试的概率为( )
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
不等式|x-1|<2的解集是( )
| A、(-2,2) |
| B、(-∞,-2)∪(2,+∞) |
| C、(-1,3) |
| D、(-3,1) |
已知an=n+2,bn=2n-3,则数列{anbn}的前n项和Sn等于( )
A、(n+2)•2n-1-
| ||
B、
| ||
C、(n+1)•2n-2-
| ||
D、
|
 说出下列算法的结果.运行时输入3、4、5,运行结果为输出:
说出下列算法的结果.运行时输入3、4、5,运行结果为输出: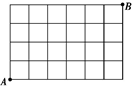 某市新城区有7条南北向街道,5条东西向街道(如图).
某市新城区有7条南北向街道,5条东西向街道(如图).