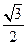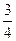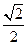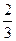题目内容
设斜率为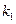 的直线
的直线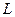 交椭圆
交椭圆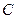 :
: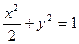 于
于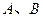 两点,点
两点,点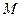 为弦
为弦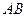 的中点,直线
的中点,直线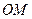 的斜率为
的斜率为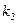 (其中
(其中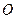 为坐标原点,假设
为坐标原点,假设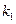 、
、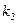 都存在).
都存在).
(1)求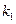 ×
×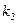 的值.
的值.
(2)把上述椭圆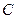 一般化为
一般化为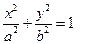 (
(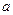 >
>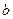 >0),其它条件不变,试猜想
>0),其它条件不变,试猜想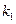 与
与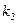 关系(不需要证明).请你给出在双曲线
关系(不需要证明).请你给出在双曲线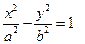 (
(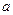 >0,
>0,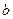 >0)中相类似的结论,并证明你的结论.
>0)中相类似的结论,并证明你的结论.
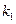 的直线
的直线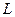 交椭圆
交椭圆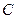 :
: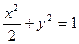 于
于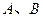 两点,点
两点,点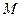 为弦
为弦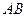 的中点,直线
的中点,直线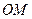 的斜率为
的斜率为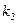 (其中
(其中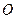 为坐标原点,假设
为坐标原点,假设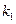 、
、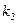 都存在).
都存在).(1)求
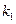 ×
×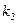 的值.
的值. (2)把上述椭圆
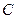 一般化为
一般化为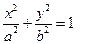 (
(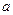 >
>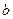 >0),其它条件不变,试猜想
>0),其它条件不变,试猜想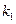 与
与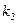 关系(不需要证明).请你给出在双曲线
关系(不需要证明).请你给出在双曲线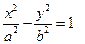 (
(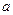 >0,
>0,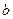 >0)中相类似的结论,并证明你的结论.
>0)中相类似的结论,并证明你的结论.(1)

(2)略
解(一):(1)设直线方程 ,代入椭圆方程并整理得:
,代入椭圆方程并整理得:
 ,
,
 ,又中点M在直线上,所以
,又中点M在直线上,所以 ,从而可得弦中点M的坐标为
,从而可得弦中点M的坐标为 ,
, ,所以
,所以
解(二)设点 ,中点
,中点 则
则


又 与
与 作差得
作差得 所以
所以
(2)对于椭圆,
已知斜率为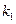 的直线
的直线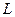 交双曲线
交双曲线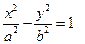 (
(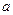 >0,
>0,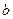 >0)于
>0)于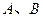 两点,点
两点,点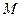 为弦
为弦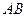 的中点,直线
的中点,直线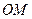 的斜率为
的斜率为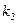 (其中
(其中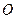 为坐标原点,假设
为坐标原点,假设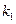 、
、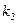 都存在).
都存在).
则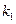 ×
×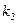 的值为
的值为 .
. 
(解一)、设直线方程为 ,代入
,代入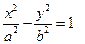 (
(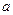 >0,
>0,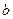 >0)方程并整理得:
>0)方程并整理得:
 ,
, ,
,
所以 ,即
,即
(解二)设点
 中点
中点
则


又因为点 在双曲线上,则
在双曲线上,则 与
与 作差得
作差得
 即
即
 ,代入椭圆方程并整理得:
,代入椭圆方程并整理得: ,
, ,又中点M在直线上,所以
,又中点M在直线上,所以 ,从而可得弦中点M的坐标为
,从而可得弦中点M的坐标为 ,
, ,所以
,所以
解(二)设点
 ,中点
,中点 则
则


又
 与
与 作差得
作差得 所以
所以
(2)对于椭圆,

已知斜率为
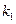 的直线
的直线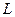 交双曲线
交双曲线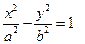 (
(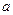 >0,
>0,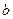 >0)于
>0)于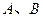 两点,点
两点,点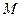 为弦
为弦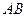 的中点,直线
的中点,直线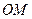 的斜率为
的斜率为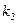 (其中
(其中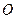 为坐标原点,假设
为坐标原点,假设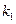 、
、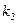 都存在).
都存在).则
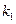 ×
×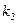 的值为
的值为 .
. 
(解一)、设直线方程为
 ,代入
,代入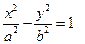 (
(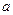 >0,
>0,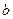 >0)方程并整理得:
>0)方程并整理得: ,
, ,
,所以
 ,即
,即
(解二)设点

 中点
中点
则



又因为点
 在双曲线上,则
在双曲线上,则 与
与 作差得
作差得 即
即

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
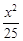 +
+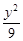 =1上一点P到左焦点F1的距离为2,M是线段PF1的中点,则M到原点O的距离等于( )
=1上一点P到左焦点F1的距离为2,M是线段PF1的中点,则M到原点O的距离等于( )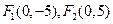 ,点
,点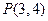 在椭圆上,求它的方程 (2)已知双曲线顶点间的距离为6,渐近线方程为
在椭圆上,求它的方程 (2)已知双曲线顶点间的距离为6,渐近线方程为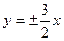 ,求它的方程.
,求它的方程.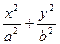 =1(a>b>0)过点(1,
=1(a>b>0)过点(1,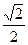 ),离心率为
),离心率为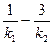 =2;
=2;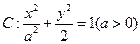 的左右焦点分别为
的左右焦点分别为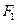 、
、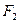 ,
,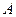 是椭圆
是椭圆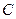 上的一点,
上的一点,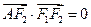 ,坐标原点
,坐标原点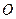 到直线
到直线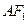 的距离为
的距离为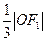 .
.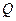 是椭圆
是椭圆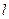 交
交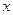 轴于点
轴于点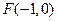 ,交
,交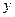 轴于点
轴于点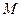 ,若
,若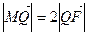 ,求直线
,求直线 ,经过椭圆
,经过椭圆 的右焦点F且斜率为
的右焦点F且斜率为 的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.(I)是否存在
的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.(I)是否存在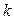 ,使对任意
,使对任意 ,总有
,总有 成立?若存在,求出所有
成立?若存在,求出所有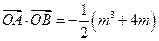 ,求实数
,求实数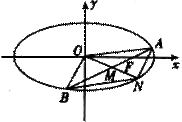
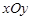 中,已知△
中,已知△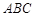 顶点
顶点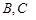
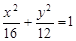 的两个焦点,顶点
的两个焦点,顶点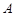 在该椭圆上,则
在该椭圆上,则 =_______________.
=_______________.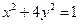 的离心率为( )
的离心率为( )