题目内容
1.直线2x-y+a=0与3x+y-3=0交于第一象限,当点P(x,y)在不等式组$\left\{\begin{array}{l}{2x-y+a≥0}\\{3x+y-3≤0}\end{array}\right.$表示的区域上运动时,m=4x+3y的最大值为8,此时n=$\frac{y}{x+3}$的最大值是( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
分析 联立方程组求得A的坐标,把A的坐标代入m=4x+3y=8求得a值,得到可行域,再由n=$\frac{y}{x+3}$的几何意义,即点B(-3,0)与P(x,y)连线的斜率求解.
解答 解:由直线2x-y+a=0与3x+y-3=0交于点A,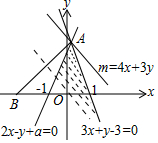
解方程组$\left\{\begin{array}{l}{2x-y+a=0}\\{3x+y-3=0}\end{array}\right.$,得A($\frac{3-a}{5},\frac{6+3a}{5}$),
将直线4x+3y=0平移经过A点时,
m取最大值,∴$4×\frac{3-a}{5}+3×\frac{6+3a}{5}=6+a=8$,得a=2.
于是,点A的坐标为($\frac{1}{5},\frac{12}{5}$),
∵n=$\frac{y}{x+3}$表示点B(-3,0)与P(x,y)连线的斜率,
由图可知,当P与点A重合时,n取最大值,
∴n的最大值为$\frac{\frac{12}{5}}{\frac{1}{5}+3}=\frac{3}{4}$.
故选:D.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
11.与球心距离为1的截球平面,所得的截面圆的面积为2π,则球的体积为( )
| A. | 8$\sqrt{3}$π | B. | 4$\sqrt{3}$π | C. | 4π | D. | 8π |
12.已知数列{an}满足an+1=$\left\{\begin{array}{l}{2{a}_{n}(0≤{a}_{n}<\frac{1}{2})}\\{2{a}_{n}-1(\frac{1}{2}≤{a}_{n}<1)}\end{array}\right.$,若a1=$\frac{6}{7}$,则a2011的值为( )
| A. | $\frac{6}{7}$ | B. | $\frac{5}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{7}$ |
16.若复数z=$\frac{2}{1+i}$+(1-i)2,则|z|等于( )
| A. | $\sqrt{10}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |
13.执行如图所示程序框图,若输出的S值为-52,则条件框内应填写( )


| A. | i<4? | B. | i<6? | C. | i<5? | D. | i>5? |
10.$\frac{1+3i}{1-i}$=( )
| A. | 1+2i | B. | -1+2i | C. | 1-2i | D. | -1-2i |
11.有如图所示的程序框图,则该程序框图表示的算法的功能是( )
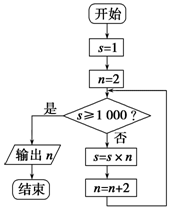

| A. | 输出使1×2×4×…×n≥1 000成立的最大整数n+2 | |
| B. | 输出使1×2×4×…×n≥1 000成立的最小整数n+2 | |
| C. | 输出使1×2×4×…×n≥1 000成立的最小整数n | |
| D. | 输出使1×2×4×…×n≥1 000成立的最大整数n |