题目内容
17.设p:|4x-3|≤1,q:(x-a)(x-a-1)≤0,若:非q是非p的充分不必要条件,求实数a取值范围.分析 求出命题p,q的等价条件,结合充分条件和必要条件的定义建立条件关系即可.
解答 解:p:|4x-3|≤1,解得$\frac{1}{2}$≤x≤1,
q:(x-a)(x-a-1)≤0,解得a≤x≤a+1,
∵非q是非p的充分不必要条件,
∴p是q的充分不必要条件,
∴$\left\{\begin{array}{l}{a≤\frac{1}{2}}\\{a+1≥1}\end{array}\right.$
解得0≤a≤$\frac{1}{2}$,
故实数a取值范围为[0,$\frac{1}{2}$]
点评 本题考查了绝对值不等式与一元二次不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
7.已知扇形的圆心角为$\frac{π}{3}$,半径为2,则扇形的弧长为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $4+\frac{2π}{3}$ |
8.若cosθ<0,且sin2θ<0,则角θ的终边所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.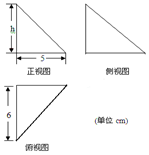 如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( )
如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( )
 如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( )
如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( )| A. | 55π | B. | 75π | C. | 77π | D. | 65π |
12.已知数列{an}满足an+1=$\left\{\begin{array}{l}{2{a}_{n}(0≤{a}_{n}<\frac{1}{2})}\\{2{a}_{n}-1(\frac{1}{2}≤{a}_{n}<1)}\end{array}\right.$,若a1=$\frac{6}{7}$,则a2011的值为( )
| A. | $\frac{6}{7}$ | B. | $\frac{5}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{7}$ |
2.已知命题“?x∈R,x2-2ax+3≥0”是假命题,则实数a的取值范围为( )
| A. | $a=\sqrt{3}$ | B. | $a>\sqrt{3}$或$a<-\sqrt{3}$ | C. | $-\sqrt{3}<a<\sqrt{3}$ | D. | $-\sqrt{3}≤a≤\sqrt{3}$ |
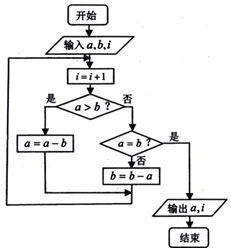 如图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0 时,则输出的i=( )
如图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0 时,则输出的i=( )