题目内容
2.已知α,β,γ为不同的平面,m,n为不同的直线,则m⊥β的一个充分条件是( )| A. | α∩γ=m,α⊥γ,β⊥γ | B. | α⊥β,β⊥γ,m⊥α | C. | α⊥β,α∩β=n,m⊥n | D. | n⊥α,n⊥β,m⊥α |
分析 在A,B,C中,满足条件的m和平面β可能平行,故A,B,C均不正确,在D中,n⊥α,n⊥β⇒α∥β,结合m⊥α知m⊥β.
解答 解:由α,β,γ为不同的平面,m,n为不同的直线,知:
在A中,α∩γ=m,α⊥γ,β⊥γ,则满足条件的m和平面β可能平行,故A错误;
在B中,α⊥β,β⊥γ,m⊥α,则满足条件的m和平面β可能平行,故A错误;
在C中,α⊥β,α∩β=n,m⊥n,满足条件的m和平面β可能平行,故C错误;
在D中,n⊥α,n⊥β⇒α∥β,结合m⊥α知m⊥β,故D正确.
故选:D.
点评 本题空间中线线、线面、面面间的位置关系,考查学生分析解决问题的能力,考查空间思维能力、数据处理能力、运算求解能力,属于中档题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
12.已知抛物线C:y2=4x的焦点是F,过点F的直线与抛物线C相交于P、Q两点,且点Q在第一象限,若2$\overrightarrow{PF}$=$\overrightarrow{FQ}$,则直线PQ的斜率是( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
13.若(x3+$\frac{1}{\sqrt{x}}$)n的展开式中含有常数项,且n的最小值为a,则${∫}_{-a}^{a}$$\sqrt{{a}^{2}-{x}^{2}}$dx=( )
| A. | 0 | B. | $\frac{686}{3}$ | C. | $\frac{49π}{2}$ | D. | 49π |
10.观察下列各式:$\frac{1}{1+2}$=$\frac{1}{3}$,$\frac{1}{1+2}$+$\frac{1}{1+2+3}$=$\frac{1}{2}$,$\frac{1}{1+2}$+$\frac{1}{1+2+3}$+$\frac{1}{1+2+3+4}$=$\frac{3}{5}$…,则$\frac{1}{1+2}$+$\frac{1}{1+2+3}$+…+$\frac{1}{1+2+…+12}$等于( )
| A. | $\frac{5}{6}$ | B. | $\frac{11}{12}$ | C. | $\frac{11}{13}$ | D. | $\frac{12}{13}$ |
17.交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为a元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的概率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有6辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选两辆车,求这两车辆中恰好有一辆事故车的概率;
②若该销售商一次购进120辆(车龄已满三年)该品牌的二手车,求一辆车盈利的平均值.
| 交强险浮动因素和浮动费率比率表 | ||
| 浮动因素 | 浮动比率 | |
| A1 | 上一个年度未发生有责任道路交通事故 | 下浮10% |
| A2 | 上两个年度未发生有责任道路交通事故 | 下浮20% |
| A3 | 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| A4 | 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| A5 | 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| A6 | 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
| 类型 | A1 | A2 | A3 | A4 | A5 | A6 |
| 数量 | 10 | 5 | 5 | 20 | 15 | 5 |
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的概率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有6辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选两辆车,求这两车辆中恰好有一辆事故车的概率;
②若该销售商一次购进120辆(车龄已满三年)该品牌的二手车,求一辆车盈利的平均值.
11.已知函数$f(x)=sin({ωx-\frac{π}{6}})+\frac{1}{2}({ω>0})$,且$f(α)=-\frac{1}{2}$,$f(β)=\frac{1}{2}$,若|α-β|的最小值为$\frac{3π}{4}$,则ω的值为( )
| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 2 |
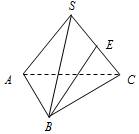 如图,三棱锥S-ABC中,若$AC=2\sqrt{3}$,SA=SB=SC=AB=BC=4,E为棱SC的中点,则直线AC与BE所成角的余弦值为$\frac{1}{4}$,直线AC与平面SAB所成的角为600.
如图,三棱锥S-ABC中,若$AC=2\sqrt{3}$,SA=SB=SC=AB=BC=4,E为棱SC的中点,则直线AC与BE所成角的余弦值为$\frac{1}{4}$,直线AC与平面SAB所成的角为600.