题目内容
在△ABC中，AB=AC=a，以BC为边向外作正△BCD，求AD最大值．
考点：解三角形
专题：计算题,解三角形
分析：设∠ABC=α，根据正弦定理得AD=2asin∠ABD，确定sin∠ABD的最大值为sin90°=1，即可求AD最大值．
解答：
解：设∠ABC=α，那么△ABD中∠ABD=60°+α，∠BDA=30°．
根据正弦定理得AD=2asin∠ABD
而我们可以知道在三角形ABC中，0°＜α＜90°，
所以∠ABD=60°+α应该大于60°而小于150°
那么sin∠ABD的最大值为sin90°=1，
故AD的最大值为2a．
根据正弦定理得AD=2asin∠ABD
而我们可以知道在三角形ABC中，0°＜α＜90°，
所以∠ABD=60°+α应该大于60°而小于150°
那么sin∠ABD的最大值为sin90°=1，
故AD的最大值为2a．
点评：本题考查正弦定理，考查学生分析解决问题的能力，比较基础．
练习册系列答案
相关题目
设集合A，B，C满足：A∪∁RB=A∪∁RC，则下列（ ）必成立．
| A、B=C |
| B、A∩B=A∩C |
| C、∁RA∩B=∁RA∩C |
| D、A∩∁RB=A∩∁RC |
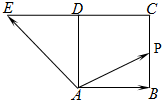如图，四边形ABCD是正方形，延长CD至E，使得DE=CD，若动点P从点A出发，沿正方形的边按如下路线运动：A→B→C→D→E→A→D，其中
为了解甲、乙两个班级某次考试的数学成绩（单位：分），从甲、乙两个班级中分别随机抽取5名学生的成绩作标本，如图是样本的茎叶图，规定：成绩不低于120分时为优秀成绩．