题目内容
4. 如图,正四棱锥P-ABCD的底面长为2,侧棱长为$\sqrt{10}$,点O为底面ABCD的中心
如图,正四棱锥P-ABCD的底面长为2,侧棱长为$\sqrt{10}$,点O为底面ABCD的中心(Ⅰ)求证:PA⊥BD;
(Ⅱ)求二面角C-PB-D的余弦值.
分析 (Ⅰ)根据线面垂直的判定定理证明BD⊥面PAC,即可证明PA⊥BD;
(Ⅱ)根据二面角的定义,作出二面角的平面角,即可求二面角C-PB-D的余弦值.
解答  证明:(Ⅰ)连接PO,
证明:(Ⅰ)连接PO,
∵底面是正方形,∴BD⊥AC,
∵PB=PD,∴PO⊥BD,
∵PO∩AC=O,
∴BD⊥面PAC,
∵PA?面PAC,
∴PA⊥BD;
(Ⅱ)同理可得AC⊥面PBD,
过O作OE⊥PB于E,
连接CE,则CE⊥PB,
即∠CEO是二面角C-PB-D的平面角,
∵正四棱锥P-ABCD的底面长为2,侧棱长为$\sqrt{10}$,
∴OC=OB=$\sqrt{2}$,PC=$\sqrt{10}$,
则PO=${\sqrt{(\sqrt{10})^{2}-(\sqrt{2})^{2}}}^{\;}$=$\sqrt{8}$=2$\sqrt{2}$,
∵S△AOB=$\frac{1}{2}PO•OB=\frac{1}{2}PB•OE$,
∴OE=$\frac{PO•OB}{PB}$=$\frac{2\sqrt{2}•\sqrt{2}}{\sqrt{10}}$=$\frac{4}{\sqrt{10}}$,
则CE=$\sqrt{O{C}^{2}+O{E}^{2}}$=$\sqrt{2+\frac{16}{10}}=\sqrt{\frac{36}{10}}$=$\frac{6}{\sqrt{10}}$,
则cos∠CEO=$\frac{OE}{CE}$=$\frac{\frac{4}{\sqrt{10}}}{\frac{6}{\sqrt{10}}}=\frac{4}{6}$=$\frac{2}{3}$,
即二面角C-PB-D的余弦值是$\frac{2}{3}$.
点评 本题主要考查直线垂直的证明,以及二面角的求解,根据线面垂直的性质定理结合二面角的平面角的定义是解决本题的关键.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案| A. | 命题“若x>y,则|x|>|y|”的逆命题 | |
| B. | 命题“若x=1,则x2+x-2=0”的否命题 | |
| C. | 命题“x>1,则x2>1”的否命题 | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题 |
| A. | $[\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2}]$ | B. | $[\frac{1}{2},1)$ | C. | $[\frac{{\sqrt{3}}}{2},1)$ | D. | $[\frac{{\sqrt{2}}}{2},1)$ |
| A. | sinθ<cosθ<tanθ | B. | sinθ<tanθ<cosθ | C. | tanθ<sinθ<cosθ | D. | 以上都不是 |
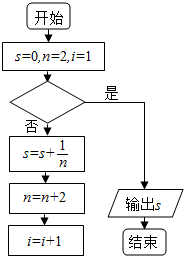
| A. | i>2016 | B. | i<2016 | C. | i>1008 | D. | i<1008 |