题目内容
5.已知函数f(log2x)=x-$\frac{1}{x}$(1)求函数f(x)的表达式,并说明函数的单调性、奇偶性(无需证明);
(2)设集合A=$\{x|x=sinθ+cosθ,θ∈(-\frac{π}{2},0)\}$,若函数y=f(x)(x∈A),且f(1-m)+f(1-m2)<0,求实数 m的取值范围;
(3)若不等式2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数 m的取值范围.
分析 (1)令a=${log}_{2}^{x}$,则x=2a,从而求出f(x)的表达式;
(2)根据三角函数的性质求出集合A,结合函数的单调性得到关于m的不等式组,求出m的范围即可;
(3)问题转化为2t(22t-$\frac{1}{{2}^{2t}}$)+m(2t-$\frac{1}{{2}^{t}}$)≥0对t∈[1,2]恒成立,根据t的范围得到2t-$\frac{1}{{2}^{t}}$>0,问题转化为2t(2t+$\frac{1}{{2}^{t}}$)+m≥0对t∈[1,2]恒成立,求出m的范围即可.
解答 解:(1)令a=${log}_{2}^{x}$,则x=2a,f(a)=2a-$\frac{1}{{2}^{a}}$,
∴f(x)=2x-$\frac{1}{{2}^{x}}$(x∈R),
f(x)是奇函数,且在R上递增;
(2)∵x=sinθ+cosθ=$\sqrt{2}$sin(θ+$\frac{π}{4}$),(θ∈(-$\frac{π}{2}$,0)),
∴θ+$\frac{π}{4}$∈(-$\frac{π}{4}$,$\frac{π}{4}$),
∴$\sqrt{2}$sin(θ+$\frac{π}{4}$)∈(-1,1),
∴A={x|-1<x<1},
由(1)f(x)是奇函数,且在R上单调递增,
对y=f(x),(x∈A),
f(1-m)+f(1-m2)<0,
有$\left\{\begin{array}{l}{1-m{<m}^{2}-1}\\{-1<1-m<1}\\{-1{<m}^{2}-1<1}\end{array}\right.$,
解得:1<m<$\sqrt{2}$;
(3)不等式2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,
即2t(22t-$\frac{1}{{2}^{2t}}$)+m(2t-$\frac{1}{{2}^{t}}$)≥0对t∈[1,2]恒成立,
∵t∈[1,2],∴2t-$\frac{1}{{2}^{t}}$>0,
∴2t(2t+$\frac{1}{{2}^{t}}$)+m≥0对t∈[1,2]恒成立,即对t∈[1,2]恒成立,
令g(t)=-(2t)2-1,t∈[1,2],
g(t)max=g(1)=-5,
∴m≥-5.
点评 本题考查了对数函数、三角函数的性质,考查转化思想,函数恒成立问题,考查学生的计算能力,是一道中档题.

| A. | $[\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2}]$ | B. | $[\frac{1}{2},1)$ | C. | $[\frac{{\sqrt{3}}}{2},1)$ | D. | $[\frac{{\sqrt{2}}}{2},1)$ |
| A. | sinθ<cosθ<tanθ | B. | sinθ<tanθ<cosθ | C. | tanθ<sinθ<cosθ | D. | 以上都不是 |
| A. | $(-1,-\frac{3}{4})$ | B. | $(-\frac{3}{4},0)$ | C. | $(\frac{3}{4},1)$ | D. | $(1,\frac{5}{4})$ |
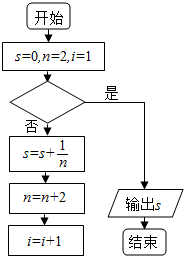
| A. | i>2016 | B. | i<2016 | C. | i>1008 | D. | i<1008 |
 某赛季甲,乙两名篮球运动员每场比赛得分情况用茎叶图表示如图:根据以上茎叶图,则甲得分的中位数是26;乙得分的众数是31和36.
某赛季甲,乙两名篮球运动员每场比赛得分情况用茎叶图表示如图:根据以上茎叶图,则甲得分的中位数是26;乙得分的众数是31和36.