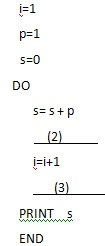题目内容
巳知全集U=R，集合M={x|-2≤x-1≤2}和N={1，3，5，7，9}的关系的韦恩（Venn）图如图所示，则阴影部分所示的集合的元素共有（ ）| A、3个 | B、2个 | C、1个 | D、无穷个 |
考点：Venn图表达集合的关系及运算
专题：集合
分析：图中阴影部分对应的集合为M∩N，然后根据集合的基本运算即可得到结论．
解答：
解：由图可知阴影部分对应的集合为M∩N，
∵M={x|-2≤x-1≤2}={x|-1≤x≤3}，N={1，3，5，7，9}，
∴M∩N={1，3}，
故选：B．
∵M={x|-2≤x-1≤2}={x|-1≤x≤3}，N={1，3，5，7，9}，
∴M∩N={1，3}，
故选：B．
点评：本题主要考查集合的基本运算，根据图象确定阴影部分对应的集合关系是解决本题的关键，比较基础．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
执行如图所示的程序框图．若输入的n的值为3，则输出的k的值为（ ）
| A、2 | B、3 | C、4 | D、5 |
已知[x）表示大于x的最小整数，例如[3）=4，[-1.2）=-1．下列命题：
①函数f（x）=[x）-x的值域是（0，1]；
②若{an}是等差数列，则{[an）}也是等差数列；
③若{an}是等比数列，则{[an）}也是等比数列；
④若x∈（1，4），则方程[x）-x=
有3个根．
正确的是（ ）
①函数f（x）=[x）-x的值域是（0，1]；
②若{an}是等差数列，则{[an）}也是等差数列；
③若{an}是等比数列，则{[an）}也是等比数列；
④若x∈（1，4），则方程[x）-x=
| 1 |
| 2 |
正确的是（ ）
| A、②④ | B、③④ | C、①③ | D、①④ |
已知平面向量
=（1，2），
=（-2，m），且
⊥
，则2
+3
=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、（8，16） |
| B、（-4，-8） |
| C、（-4，7） |
| D、（8，1） |
已知集合A={1，2，3，4}，B={2，4，6}，则A∩B的元素个数是（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
若抛物线C：y2=2px（p＞0）上一点到焦点和x轴的距离分别为5和3，则此抛物线的方程为（ ）
| A、y2=2x | ||
B、y2=（
| ||
| C、y2=2x或y2=18x | ||
D、y2=3x或y2=（
|
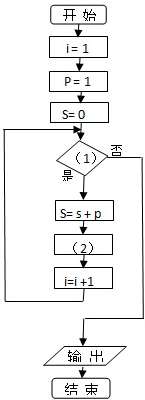给出50个数，1，2，4，7，11，…，其规律是：第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，…，以此类推．要求计算这50个数的和．先将右面给出的程序框图补充完整，再将与其功能相当的程序语言补充完整，把答案写在下面空格上．