题目内容
4.若实数x、y、m满足|x-m|<|y-m|,则称x比y接近m.(1)若2x比1接近3,求x的取值范围;
(2)已知函数f(x)定义域D=(-∞,0)∪(0,1)∪(1,3)∪(3,+∞),对于任意的x∈D,f(x)等于x2-2x与x中接近0的那个值,写出函数f(x)的解析式,若关于x的方程f(x)-a=0有两个不同的实数根,求出a的取值范围;
(3)已知a,b∈R,m>0且a≠b,求证:$\frac{a+mb}{m+1}$比$\sqrt{\frac{{{a^2}+m{b^2}}}{m+1}}$接近0.
分析 (1)直接根据定义,问题等价为|2x-3|<|1-3|,解出即可;
(2)先求出函数f(x)的解析式并画出函数图象,再运用数形结合的方法,求a的取值范围;
(3)直接运用作差法比较两式的大小.
解答 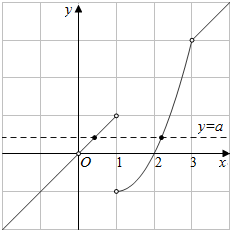 解:(1)因为2x比1接近3,所以|2x-3|<|1-3|,
解:(1)因为2x比1接近3,所以|2x-3|<|1-3|,
即|2x-3|<2,解得$\frac{1}{2}$<x<$\frac{5}{2}$,
所以,x的取值范围为:($\frac{1}{2}$,$\frac{5}{2}$);
(2)分类讨论如下:
①当x2-2x比x接近于0时,|x2-2x|<|x|,
解得,x∈(1,3),
②当x比x2-2x接近于0时,|x2-2x|>|x|,
解得,x∈(-∞,0)∪(0,1)∪(3,+∞),
所以,f(x)=$\left\{\begin{array}{l}{x^2-2x,x∈(1,3)}\\{x,x∈(-∞,0)∪(0,1)∪(3,+∞)}\end{array}\right.$,
画出f(x)的图象,如右图,
因为方程f(x)=a有两个实根,根据函数图象得,
a∈(-1,0)∪(0,1);
(3)对两式$\frac{a+mb}{m+1}$,$\sqrt{\frac{{{a^2}+m{b^2}}}{m+1}}$平方作差得,
△=($\sqrt{\frac{{{a^2}+m{b^2}}}{m+1}}$)2-($\frac{a+mb}{m+1}$)2
=$\frac{(m+1)(a^2+mb^2)-(a+bm)^2}{(m+1)^2}$=$\frac{m(a-b)^2}{(m+1)^2}$,
因为a,b∈R,m>0且a≠b,所以,△>0恒成立,
所以,$\sqrt{\frac{{{a^2}+m{b^2}}}{m+1}}$>|$\frac{a+mb}{m+1}$|,
即$\frac{a+mb}{m+1}$比$\sqrt{\frac{{{a^2}+m{b^2}}}{m+1}}$接近0.
点评 本题主要考查了绝对值不等式的解法,分段函数解析式的确定,和不等式的证明,体现了分类讨论,数形结合的解题思想,属于难题.

| A. | 3 | B. | 1 | C. | -5 | D. | -6 |
| A. | sinα+cosβ=1 | B. | (sinα+cosα)2=1 | C. | sin2α+cos2α=1 | D. | sin2α+cos2β=1 |
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
用茎叶图表示甲,乙两个成绩;并根据茎叶图分析甲、乙两人成绩;
(2)某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(Ⅱ)预计在今后的销售中,销量与单价仍然服从(I)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
 ,则不等式
,则不等式 的解集为( )
的解集为( ) B.
B.
 D.(1,2)
D.(1,2)