题目内容
已知函数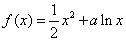 .
.
(Ⅰ)若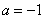 ,求函数
,求函数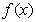 的极值,并指出是极大值还是极小值;
的极值,并指出是极大值还是极小值;
(Ⅱ)若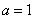 ,求证:在区间
,求证:在区间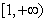 上,函数
上,函数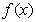 的图像在函数
的图像在函数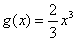 的图像的下方.
的图像的下方.
解析:(Ⅰ)解由于函数f(x)的定义域为(0,+∞), 1分
当a=-1时,f′(x)=x-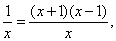 2分
2分
令f′(x)=0得x=1或x=-1(舍去), 3分
当x∈(0,1)时,f′(x)<0, 因此函数f(x)在(0,1)上是单调递减的, 4分
当x∈(1,+∞)时,f′(x)>0,因此函数f(x)在(1,+∞)上是单调递增的, 5分
则x=1是f(x)极小值点,
所以f(x)在x=1处取得极小值为f(1)=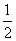 6分
6分
(Ⅱ)证明 设F(x)=f(x)-g(x)=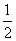 x2+ln x-
x2+ln x-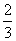 x3,
x3,
则F′(x)=x+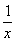 -2x2=
-2x2=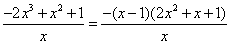 , 8分
, 8分
当x>1时,F′(x)<0, 9分
故f(x)在区间[1,+∞)上是单调递减的, 10分
又F(1)=-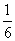 <0, 11分
<0, 11分
∴在区间[1,+∞)上,F(x)<0恒成立.即f(x)—g(x)<0恒成立
即f(x)<g(x)恒成立.
因此,
当a=1时,在区间[1,+∞)上,函数f(x)的图像在函数g(x)图像的下方. 12分

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
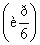 +m=0,曲线C2的参数方程为
+m=0,曲线C2的参数方程为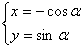 (0<α<π),若曲线C1与C2有两个不同的交点,则实数m的取值范围是____________.
(0<α<π),若曲线C1与C2有两个不同的交点,则实数m的取值范围是____________.
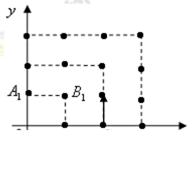 2010年,我国南方省市遭遇旱涝灾害,为防洪抗旱,某地区大面积植树造林,如图,在区域
2010年,我国南方省市遭遇旱涝灾害,为防洪抗旱,某地区大面积植树造林,如图,在区域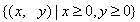 内植树,第一棵树在
内植树,第一棵树在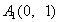 点,第二棵树在
点,第二棵树在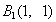 点,第三棵树在
点,第三棵树在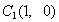 点,第四棵树在
点,第四棵树在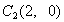 点,接着按图中箭头方向,每隔一个单位种一颗树,那么,第2014棵树所在的点的坐标是( )
点,接着按图中箭头方向,每隔一个单位种一颗树,那么,第2014棵树所在的点的坐标是( ) 的前
的前 项和
项和 (
( ),则
),则 的值是__________.
的值是__________.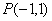 和点
和点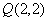 ,若直线
,若直线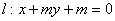 与线段
与线段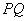 不相交,则实数
不相交,则实数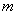 的取值范围是 .
的取值范围是 . 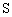 店经销
店经销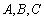 三种排量的汽车,其中
三种排量的汽车,其中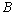 种排量汽车的概率;
种排量汽车的概率;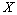 ,求
,求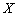 的分布列及数学期望.
的分布列及数学期望.