题目内容
已知点P(a,a)(a为常数),点Q(
,
),若点R在函数f(x)=
(x>0)图象上移动时不等式|PR|≥|PQ|恒成立,则实数a的取值范围是( )
| 2 |
| 2 |
| 2 |
| x |
A、a≥2
| ||||
B、a≤2
| ||||
C、-2
| ||||
D、a≤-2
|
考点:函数恒成立问题
专题:函数的性质及应用
分析:依题意知,点P(a,a)(a为常数),点Q(
,
)均为直线y=x上的点,作出图形,易知a<
时,不等式|PR|≥|PQ|恒成立;当a≥
时,设R(x,
),
通过构造函数g(t)=t2-2at+4
a-8=(t-a)2+4
a-8-a2(t≥2
),其对称轴方程为t=a,利用二次函数的单调性质分类讨论,来解决函数恒成立问题即可.
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| x |
通过构造函数g(t)=t2-2at+4
| 2 |
| 2 |
| 2 |
解答:
解:∵点P(a,a)(a为常数),点Q(
,
)均为直线y=x上的点,点R在函数f(x)=
(x>0)图象上移动,
作图如下:
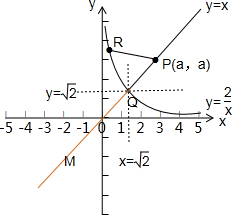
由图可知,当点P在射线QM(红线)上移动,即a<
时,不等式|PR|≥|PQ|恒成立;
当a≥
时,设R(x,
),
则|PR|=
,又|PQ|=|PO|-|OQ|=
a-
=
a-2>0,
∴不等式|PR|≥|PQ|恒成立?
≥
a-2恒成立?(x-a)2+(
-a)2≥2a2-4
a+4恒成立;
整理得:(x+
)2-2a(x+
)+4
a-8≥0恒成立;
令t=x+
,则t≥2
,
构造函数g(t)=t2-2at+4
a-8=(t-a)2+4
a-8-a2(t≥2
),
若
≤a≤2
,y=g(t)在[2
,+∞)上单调递增,
要使g(t)=(t-a)2+4
a-8-a2≥0恒成立,只需g(t)min=g(2
)=(2
)2-2×2
a+4
a-8=0≥0成立,显然成立,
∴
≤a≤2
;
若a>2
,同理可得,t=a时y=g(t)取得最小值,即g(t)min=g(a)=4
a-8-a2=-(a-2
)2<0,不合题意;
综上所述,实数a的取值范围是a≤2
;
故选:B.
| 2 |
| 2 |
| 2 |
| x |
作图如下:

由图可知,当点P在射线QM(红线)上移动,即a<
| 2 |
当a≥
| 2 |
| 2 |
| x |
则|PR|=
(x-a)2+(
|
| 2 |
(
|
| 2 |
∴不等式|PR|≥|PQ|恒成立?
(x-a)2+(
|
| 2 |
| 2 |
| x |
| 2 |
整理得:(x+
| 2 |
| x |
| 2 |
| x |
| 2 |
令t=x+
| 2 |
| x |
| 2 |
构造函数g(t)=t2-2at+4
| 2 |
| 2 |
| 2 |
若
| 2 |
| 2 |
| 2 |
要使g(t)=(t-a)2+4
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
∴
| 2 |
| 2 |
若a>2
| 2 |
| 2 |
| 2 |
综上所述,实数a的取值范围是a≤2
| 2 |
故选:B.
点评:本题考查函数的图象与性质的综合应用,着重考查函数恒成立问题,突出等价转化思想、函数方程思想、分类讨论思想、数形结合思想的综合运用,属于难题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
在等比数列 {an} 中,a5a7=2,a2+a10=3,则
( )
| a12 |
| a4 |
| A、2 | ||
B、
| ||
C、2或
| ||
D、-2 或-
|
要使函数y=x2-2ax+1在[1,2]上存在反函数,则a的取值范围是 ( )
| A、a≤1 | B、a≥2 |
| C、a≤1或a≥2 | D、1≤a≤2 |
函数f(x)=x2-3x-4的零点是( )
| A、(1,-4) |
| B、(4,-1) |
| C、1,-4 |
| D、4,-1 |
 为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95),由此得到频率分布直方图如图所示,则这20名工人中一天生产该产品数量在[55,75)的人数是
为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95),由此得到频率分布直方图如图所示,则这20名工人中一天生产该产品数量在[55,75)的人数是