题目内容
6．已知函数$f（x）=ax+{log_b}\frac{1+x}{1-x}+3$（a∈R，b＞0且b≠1），若f[lg（log210）]=5，则f[lg（lg2）]=（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 5 |
分析 由已知可得f（x）+f（-x）=6，进而得到答案．
解答 解：∵$f（x）=ax+{log_b}\frac{1+x}{1-x}+3$，
∴$f（-x）=-ax+lo{g}_{b}\frac{1-x}{1+x}+3$=$-ax-lo{g}_{b}\frac{1+x}{1-x}+3$，
即f（x）+f（-x）=6，
∵lg（log210）=-lg（lg2），f[lg（log210）]=5，
∴f[lg（lg2）]=1，
故选：A
点评 本题考查的知识点是函数求值，根据已知得到f（x）+f（-x）=6，是解答的关键．
练习册系列答案
相关题目
16．命题“?x∈R，f（x）＜g（x）＜h（x）”的否定形式是（ ）
| A． | ?x0∈R，f（x0）≥g（x0）≥h（x0） | B． | ?x0∈R，f（x0）≥g（x0）或g（x0）≥h（x0） | ||
| C． | ?x∈R，f（x）≥g（x）≥h（x） | D． | ?x∈R，f（x）≥g（x）或g（x）≥h（x） |
17．两条直线l1：2x+y-1=0和l2：x-2y+4=0的交点为（ ）
| A． | （$\frac{2}{5}$，$\frac{9}{5}$） | B． | （-$\frac{2}{5}$，$\frac{9}{5}$） | C． | （$\frac{2}{5}$，-$\frac{9}{5}$） | D． | （-$\frac{2}{5}$，-$\frac{9}{5}$） |
14．
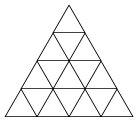设有一个等边三角形网格，其中各个最小等边三角形的边长都是4$\sqrt{3}$cm，现用直径等于2cm的硬币投掷到此网格上，则硬币落下后与格线没有公共点的概率为（ ）
设有一个等边三角形网格，其中各个最小等边三角形的边长都是4$\sqrt{3}$cm，现用直径等于2cm的硬币投掷到此网格上，则硬币落下后与格线没有公共点的概率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{8}$ | D． | $\frac{1}{3}$ |
1．已知条件p：|x+1|＞2，条件q：|x|＞a，且￢p是￢q的必要不充分条件，则实数a的取值范围是（ ）
| A． | 0≤a≤1 | B． | 1≤a≤3 | C． | a≤1 | D． | a≥3 |
以vcm3/秒的恒定速度往高为H的杯中注水，水深h是时间t的函数，其图象如图，则此杯的形状可能是（ ）
