��Ŀ����
8����ֱ������ϵxOy�У�����C�IJ�������Ϊ$\left\{\begin{array}{l}{x=1+cos��}\\{y=sin��}\end{array}\right.$����Ϊ����������������ԭ��Ϊ���㣬x��������Ϊ����ļ�����ϵ�У�ֱ��l�ļ����귽��Ϊ��sin��$��+\frac{��}{4}$��=2$\sqrt{2}$������������C��ֱ��l�ڸ�ֱ������ϵ�µ���ͨ���̣�
������A������C�ϣ�����B��ֱ��l�ϣ�����P������Ϊ��-2��2������|PB|+|AB|����Сֵ��
���� ����������C�IJ����������������C��ֱ�����귽�̣���ֱ��l�ļ����귽�������ֱ��lֱ�����귽�̣�
��������P��-2��2����������������빫ʽ�����|PB|+|AB|ȡ��Сֵ��
��� 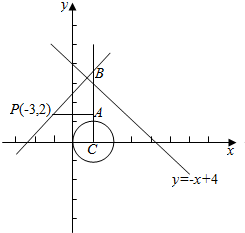 �⣺��������C�IJ�������Ϊ$\left\{\begin{array}{l}{x=1+cos��}\\{y=sin��}\end{array}\right.$����Ϊ��������
�⣺��������C�IJ�������Ϊ$\left\{\begin{array}{l}{x=1+cos��}\\{y=sin��}\end{array}\right.$����Ϊ��������
������C��ֱ�����귽��Ϊ��x-1��2+y2=1��
��ֱ��l�ļ����귽��Ϊ��sin��$��+\frac{��}{4}$��=2$\sqrt{2}$��
��$��sin��cos\frac{��}{4}+��cos��sin\frac{��}{4}$=2$\sqrt{2}$��
��sin��+��cos��=4��
��ֱ��lֱ�����귽��Ϊx+y-4=0��
������ͼ��P����y=-x+4�ԳƵ�P�䣨x��y����
|P��C|-r=P��A=P��A=|P��B|=P��B|+|A��B|��
��ʱP��BA���ɹ��ߣ�|PB|+|AB|ȡ��Сֵ��
��$\frac{y+2}{2}=-\frac{x-2}{2}+4$�����x=2��y=6��
��|PA��|=$\sqrt{36+1}$-1=$\frac{y-2}{x+2}=1$��
��$\sqrt{37}-1$��
��|PB|+|AB|����Сֵ��$\sqrt{37}-1$����
���� ���⿼��ֱ�������ߵ�ֱ�����귽�̵����������߶κ͵���Сֵ�����ǻ����⣬����ʱҪע���������빫ʽ�ĺ������ã�

 ��У����ϵ�д�
��У����ϵ�д�
| A�� | 30�� | B�� | 45�� | C�� | 60�� | D�� | 90�� |
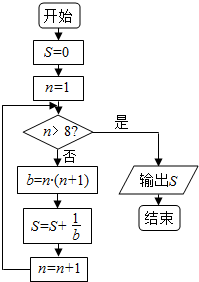
| A�� | $\frac{7}{8}$ | B�� | $\frac{9}{10}$ | C�� | $\frac{8}{9}$ | D�� | $\frac{10}{11}$ |
| A�� | ��0��1�� | B�� | ��1��2�� | C�� | ��2��3�� | D�� | ��3��4�� |