题目内容
9.直线y=2x-3与x轴交点坐标为($\frac{3}{2}$,0);与y轴交点坐标为(0,-3);在其定义域上是单调增函数.分析 令y=0,求出x的值得直线与x轴交点坐标,令x=0求出y的值得直线与y轴交点坐标;
根据一次函数的图象得出函数其定义域上的单调性.
解答 解:直线y=2x-3与x轴交点坐标为($\frac{3}{2}$,0);
与y轴交点坐标为(0,-3);
在定义域R上是单调增函数.
故答案为:($\frac{3}{2}$,0),(0,-3),增.
点评 本题考查了直线的方程与坐标轴交点的问题,也考查了一次函数的图象与性质的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.如果对数函数y=logax的图象经过点P($\frac{1}{8}$,3),则底a=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
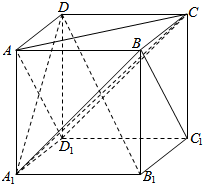 如图所示,在正方体ABCD-A1B1C1D1中,下列结论中正确的个数是( )
如图所示,在正方体ABCD-A1B1C1D1中,下列结论中正确的个数是( ) 有一面足够长的墙,现用一36米长的篱笆围成如图所示的四个面积相等的猪圈,那么猪圈的最大总面积为$\frac{324}{5}$.
有一面足够长的墙,现用一36米长的篱笆围成如图所示的四个面积相等的猪圈,那么猪圈的最大总面积为$\frac{324}{5}$.