题目内容
14.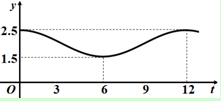 某企业一天中不同时刻的用电量y(万千瓦时)关于时间t(小时,0≤t≤24)的函数y=f(t)近似满足f(t)=Asin(ωt+φ)+B,(A>0,ω>0,0<φ<π).如图是函数y=f(t)的部分图象(t=0对应凌晨0点).
某企业一天中不同时刻的用电量y(万千瓦时)关于时间t(小时,0≤t≤24)的函数y=f(t)近似满足f(t)=Asin(ωt+φ)+B,(A>0,ω>0,0<φ<π).如图是函数y=f(t)的部分图象(t=0对应凌晨0点).(Ⅰ)根据图象,求A,ω,φ,B的值;
(Ⅱ)由于当地冬季雾霾严重,从环保的角度,既要控制火力发电厂的排放量,电力供应有限;又要控制企业的排放量,于是需要对各企业实行分时拉闸限电措施.已知该企业某日前半日能分配到的供电量g(t)(万千瓦时)与时间t(小时)的关系可用线性函数模型g(t)=-2t+25(0≤t≤12)模拟.当供电量小于该企业的用电量时,企业就必须停产.初步预计停产时间在中午11点到12点间,为保证该企业既可提前准备应对停产,又可尽量减少停产时间,请从这个初步预计的时间段开始,用二分法帮其估算出精确到15分钟的停产时间段.
分析 (Ⅰ)根据图象最值求A,B,根据周期求出ω,利用特殊点求出φ的值;
(Ⅱ)h(t)=f(t)-g(t),设h(t0)=0,则t0为该企业的停产时间.易知h(t)在(11,12)上是单调递增函数,确定t0∈(11.25,11.5).即可得出结论.
解答 解:(Ⅰ)由图知$T=12=\frac{2π}{ω}$,∴$ω=\frac{π}{6}$. (1分)
$A=\frac{{{y_{max}}-{y_{min}}}}{2}=\frac{2.5-1.5}{2}=\frac{1}{2}$,$B=\frac{{{y_{max}}+{y_{min}}}}{2}=\frac{2.5+1.5}{2}=2$.(3分)
∴$y=\frac{1}{2}sin(\frac{π}{6}x+φ)+2$.代入(0,2.5),得$φ=\frac{π}{2}+2kπ$,
又0<φ<π,∴$φ=\frac{π}{2}$. (5分)
综上,$A=\frac{1}{2}$,$ω=\frac{π}{6}$,$φ=\frac{π}{2}$,B=2. 即$f(t)=\frac{1}{2}sin(\frac{π}{6}t+\frac{π}{2})+2$. (6分)
(Ⅱ)由(Ⅰ)知$f(t)=\frac{1}{2}sin(\frac{π}{6}t+\frac{π}{2})+2=\frac{1}{2}cos\frac{π}{6}t+2$.
令h(t)=f(t)-g(t),
设h(t0)=0,则t0为该企业的停产时间.易知h(t)在(11,12)上是单调递增函数.
由h(11)=f(11)-g(11)<0,h(12)=f(12)-g(12)>0,
又$h(11.5)=f(11.5)-g(11.5)=\frac{1}{2}cos\frac{23π}{12}+2-2=\frac{1}{2}cos(-\frac{π}{12})>0$,则t0∈(11,11.5).
即11点到11点30分之间(大于15分钟)
又$h(11.25)=f(11.25)-g(11.25)=\frac{1}{2}cos\frac{45π}{24}+2-2.5<\frac{1}{2}×1-0.5=\frac{1}{2}-0.5=0$,
则t0∈(11.25,11.5).即11点15分到11点30分之间(正好15分钟).(11分)
答:估计在11点15分到11点30分之间的时间段停产.(12分)
点评 本题考查三角函数图象与性质,考查三角函数解析式的确定,考查学生的计算能力,属于中档题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案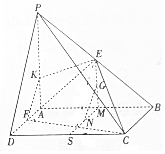 在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为矩形,点E,F,M,S分别为棱PB,AD,AB,CD的中点,G为线段EM的中点,且PA=AB=2AD=4,N为SM上一点,且NG∥平面CEF.
在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为矩形,点E,F,M,S分别为棱PB,AD,AB,CD的中点,G为线段EM的中点,且PA=AB=2AD=4,N为SM上一点,且NG∥平面CEF.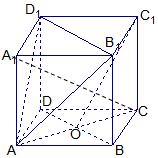 已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.求证:
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.求证:
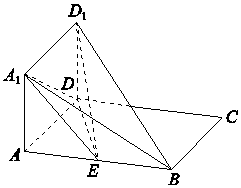 如图所示,四边形ABCD和四边形ADD1A1均为矩形且所在的平面互相垂直,E为线段AB的中点.
如图所示,四边形ABCD和四边形ADD1A1均为矩形且所在的平面互相垂直,E为线段AB的中点.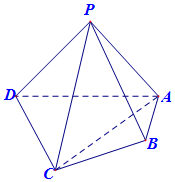 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.