题目内容
17.若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,求a,b的值.分析 求出函数的导数,求得切线的斜率,再由切线方程,可得斜率和切点坐标,进而得到a,b的值.
解答 解:y=x2+ax+b的导数为y′=2x+a,
在点(0,b)处的切线斜率为k=a,
由切线方程是x-y+1=0,
可得a=1,b=1.
点评 本题考查导数的运用:求切线的方程,考查导数的几何意义:函数在某点处的导数即为曲线在该点处的切线的斜率,属于基础题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
5.给出下列三个问题:
①从高二(3)班60名学生中,抽出8名学生去参加座谈
②将全年级学号尾数为5的同学的作业收来检查
③甲乙丙三个车间生产了同一种产品分别为60件,40件、30件,为了解产品质量,取一个容量为13的样本调查
则以上问题适宜采用的抽样方法分别是( )
①从高二(3)班60名学生中,抽出8名学生去参加座谈
②将全年级学号尾数为5的同学的作业收来检查
③甲乙丙三个车间生产了同一种产品分别为60件,40件、30件,为了解产品质量,取一个容量为13的样本调查
则以上问题适宜采用的抽样方法分别是( )
| A. | 简单随机抽样、系统抽样、分层抽样 | B. | 简单随机抽样、分层抽样、系统抽样 | ||
| C. | 系统抽样、分层抽样、简单随机抽样 | D. | 系统抽样、简单随机抽样、分层抽样 |
12.某公司对其50名员工的工作积极性和参加团队活动的态度进行了调查,统计数据得到如下2×2列联表:
(参考数据:
K2=$\frac{m(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$ )
则至少有99.9%的把握可以认为员工的工作积极性与参加团队活动的态度有关.(请用百分数表示)
| 积极参加团队活动 | 不太积极参加团队活动 | 合计 | |
| 工作积极性高 | 18 | 7 | 25 |
| 工作积极性不高 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
| p(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
则至少有99.9%的把握可以认为员工的工作积极性与参加团队活动的态度有关.(请用百分数表示)
9.函数y=2x+1-1的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
6.在棱长为a正方体ABCD-A1B1C1D1中,AC1和BD1相交于点O,则有( )
| A. | $\overrightarrow{AB}•\overrightarrow{{A_1}C}=2{a^2}$ | B. | $\overrightarrow{AB}•\overrightarrow{AC}=\sqrt{2}{a^2}$ | C. | $\overrightarrow{AB}•\overrightarrow{{A_1}O}=\frac{1}{2}{a^2}$ | D. | $\overrightarrow{BC}•\overrightarrow{AO}={a^2}$ |
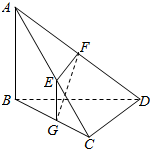 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,E,F,G分别是AC,AD,BC的中点.求证:
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,E,F,G分别是AC,AD,BC的中点.求证: