题目内容
6.在棱长为a正方体ABCD-A1B1C1D1中,AC1和BD1相交于点O,则有( )| A. | $\overrightarrow{AB}•\overrightarrow{{A_1}C}=2{a^2}$ | B. | $\overrightarrow{AB}•\overrightarrow{AC}=\sqrt{2}{a^2}$ | C. | $\overrightarrow{AB}•\overrightarrow{{A_1}O}=\frac{1}{2}{a^2}$ | D. | $\overrightarrow{BC}•\overrightarrow{AO}={a^2}$ |
分析 以D为坐标原点,以DA为x轴,以DC为y轴,以DD1为轴,建立空间坐标系,如图所示,分别根据向量的数量积的运算法则计算即可.
解答  解:在正方体ABCD-A1B1C1D1中,棱长为a,令a=1,
解:在正方体ABCD-A1B1C1D1中,棱长为a,令a=1,
以D为坐标原点,以DA为x轴,以DC为y轴,以DD1为轴,建立空间坐标系,如图所示,
∴A(1,0,0),B(1,1,0),C(0,1,0),A1(1,0,1),C1(0,1,1),D1(0,0,1),
∴O($\frac{1}{2}$,$\frac{1}{2}$,$\frac{1}{2}$),
∴$\overrightarrow{AB}$=(0,1,0),$\overrightarrow{AC}$=(-1,1,0),$\overrightarrow{{A}_{1}C}$=(-1,1,-1),$\overrightarrow{{A}_{1}O}$=(-$\frac{1}{2}$,$\frac{1}{2}$,-$\frac{1}{2}$),$\overrightarrow{BC}$=(-1,0,0),$\overline{AO}$=(-$\frac{1}{2}$,$\frac{1}{2}$,$\frac{1}{2}$),
∴$\overrightarrow{AB}$•$\overrightarrow{{A}_{1}C}$=1,$\overrightarrow{AB}•\overrightarrow{AC}$=1,$\overrightarrow{AB}•\overrightarrow{{A}_{1}O}$=$\frac{1}{2}$,$\overrightarrow{BC}•\overrightarrow{AO}$=$\frac{1}{2}$,
∴只有C正确,
故选:C.
点评 本题考查了空间向量的计算问题,建立空间坐标系是关键,属于基础题.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案| A. | λ$≥\frac{1}{3}$ | B. | λ$>\frac{1}{3}$ | C. | λ$≥\frac{4}{3}$ | D. | λ$>\frac{4}{3}$ |
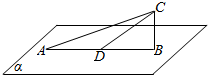 如图,平面α⊥平面ABC,D为线段AB的中点,|AB|=2$\sqrt{3}$,∠CDB=30°,P为面α内的动点,且P到直线CD的距离为1,则∠APB的最大值为 )
如图,平面α⊥平面ABC,D为线段AB的中点,|AB|=2$\sqrt{3}$,∠CDB=30°,P为面α内的动点,且P到直线CD的距离为1,则∠APB的最大值为 )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
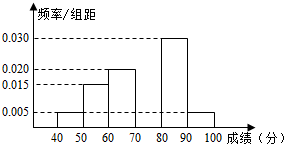 某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]),
某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]),