题目内容
5.已知函数y=f(x)的定义域为R,且y=f(x-1)的图象关于x=1对称,当x≥0时,f(x)=$\left\{\begin{array}{l}{\frac{5}{4}tan\frac{πx}{4},0≤x≤1}\\{(\frac{1}{4})^{x}+1,x>1}\end{array}\right.$若关于x的方程5[f(x)]2-(5a+6)f(x)+6a=0(a∈R)有且仅有6个不同实数根,则实数a的取值范围是a=$\frac{5}{4}$或0<a<1.分析 易知函数y=f(x)是R上的偶函数,作函数y=f(x)的图象,由方程化简可解得f(x)=a或f(x)=$\frac{6}{5}$,从而转化为函数的图象的交点的个数,从而解得.
解答 解:∵函数y=f(x)的定义域为R,且y=f(x-1)的图象关于x=1对称,
∴函数y=f(x)是R上的偶函数,
故作函数y=f(x)的图象如下,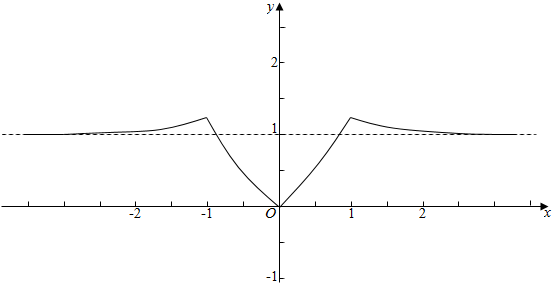 ,
,
∵5[f(x)]2-(5a+6)f(x)+6a=0,
∴(f(x)-a)(5f(x)-6)=0,
∴f(x)=a或f(x)=$\frac{6}{5}$,
∵1<$\frac{6}{5}$<$\frac{5}{4}$,∴f(x)=$\frac{6}{5}$有四个不同的解,
∴f(x)=a有两个不同的解,
即y=f(x)与y=a的图象有两个不同的交点,
故a=$\frac{5}{4}$或0<a<1;
故答案为:a=$\frac{5}{4}$或0<a<1.
点评 本题考查了函数的性质的判断及函数的图象的作法与应用,同时考查了方程与函数的关系应用及数形结合的思想方法应用,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
10.执行如图所示的程序框图,则输出的结果是( )


| A. | $\frac{19}{20}$ | B. | $\frac{20}{21}$ | C. | $\frac{21}{22}$ | D. | $\frac{22}{23}$ |
14.函数y=$\left\{\begin{array}{l}{2x,x≥0}\\{-{x}^{2},x<0}\\{\;}\end{array}\right.$的反函数是( )
| A. | y=$\left\{\begin{array}{l}{\frac{x}{2},x≥0}\\{\sqrt{-x},x<0}\\{\;}\end{array}\right.$ | B. | y=$\left\{\begin{array}{l}{\frac{x}{2},x≥0}\\{-\sqrt{-x},x<0}\\{\;}\end{array}\right.$ | ||
| C. | y=$\left\{\begin{array}{l}{2x,x≥0}\\{\sqrt{-x},x<0}\end{array}\right.$ | D. | y=$\left\{\begin{array}{l}{2x,x≥0}\\{-\sqrt{-x},x<0}\\{\;}\end{array}\right.$ |
 如图所示,四边形ABCD是腰长为2的等腰梯形,其上底长为2,下底长为4,E是腰BC上一点,P为上底CD上一点,且$\overrightarrow{BE}$=$λ\overrightarrow{BC}$,$\overrightarrow{DP}$=$λ\overrightarrow{DC}$,λ∈[0,1],则$\overrightarrow{AP}$•$\overrightarrow{AE}$的取值范围是[4,10].
如图所示,四边形ABCD是腰长为2的等腰梯形,其上底长为2,下底长为4,E是腰BC上一点,P为上底CD上一点,且$\overrightarrow{BE}$=$λ\overrightarrow{BC}$,$\overrightarrow{DP}$=$λ\overrightarrow{DC}$,λ∈[0,1],则$\overrightarrow{AP}$•$\overrightarrow{AE}$的取值范围是[4,10].