题目内容
1.已知函数f(x)=2ax2+3b(a,b∈R),若对于任意x∈[-1,1],都有|f(x)|≤1成立,则ab的最大值是$\frac{1}{24}$.分析 由对于任意x∈[-1,1],都有|f(x)|≤1成立,可得(a,b)对应的可行域,进而根据基本不等式得到ab的最大值.
解答 解:函数f(x)=2ax2+3b图象的顶点为(0,3b),
若若对于任意x∈[-1,1],都有|f(x)|≤1成立,
则$\left\{\begin{array}{l}-1≤2a+3b≤1\\-1≤3b≤1\end{array}\right.$,
其对应的平面区域如下图所示: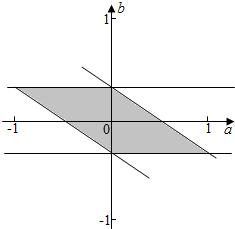
令Z=ab,则在第一,三象限a,b同号时ab取最大值,
由2a+3b=1,a>0,b>0得:ab≤$\frac{(2a+3b)^{2}}{24}$=$\frac{1}{24}$,
故答案为:$\frac{1}{24}$
点评 本题考查的知识点是恒成立问题,线性规划,基本不等式,是不等式和函数的综合应用,难度中档.

练习册系列答案
相关题目
12.已知集合U={1,2,3,4,5,6,7},集合A={2,4,5},则∁UA=( )
| A. | ∅ | B. | {1,3,5} | C. | {1,3,6,7} | D. | {1,3,5,7} |
6.已知sin(α-β)=-$\frac{12}{13}$,cosβ=-$\frac{4}{5}$,且α-β∈(π,$\frac{3π}{2}$),β∈($\frac{π}{2}$,π),求sinα.
10.在三角形ABC中,内角A,B,C所对的边分别为a,b,c,若acosA=bsinB,则sinAcosA+cos2B等于( )
| A. | -$\frac{1}{2}$ | B. | 1 | C. | -1 | D. | $\frac{1}{2}$ |
5. 将偶数按如图所示的规律排列下去,且用amn表示位于从上到下第m行,从左到右n列的数,比如a22=6,a43=18,若amn=2016,则有 ( )
将偶数按如图所示的规律排列下去,且用amn表示位于从上到下第m行,从左到右n列的数,比如a22=6,a43=18,若amn=2016,则有 ( )
 将偶数按如图所示的规律排列下去,且用amn表示位于从上到下第m行,从左到右n列的数,比如a22=6,a43=18,若amn=2016,则有 ( )
将偶数按如图所示的规律排列下去,且用amn表示位于从上到下第m行,从左到右n列的数,比如a22=6,a43=18,若amn=2016,则有 ( )| A. | m=44,n=28 | B. | m=44,n=29 | C. | m=45,n=28 | D. | m=45,n=29 |

 设函数f(x)=$\left\{\begin{array}{l}{{3}^{x}-a,x<1}\\{{x}^{2}-4ax+3{a}^{2},x≥1}\end{array}\right.$
设函数f(x)=$\left\{\begin{array}{l}{{3}^{x}-a,x<1}\\{{x}^{2}-4ax+3{a}^{2},x≥1}\end{array}\right.$