题目内容
12.已知过原点的直线l与圆C:x2+y2-6x+5=0相交于不同的两点A、B,且线段AB中点坐标为(2,$\sqrt{2}$),则弦长为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 通过将圆C的一般式方程化为标准方程,得出圆心与半径,再利用勾股定理求出弦长.
解答 解:圆C:x2+y2-6x+5=0,整理,得其标准方程为:(x-3)2+y2=4,
∴圆C的圆心坐标为(3,0),半径为2,
∵线段AB中点坐标为D(2,$\sqrt{2}$),
∴|CD|=$\sqrt{1+2}$=$\sqrt{3}$,
∴|AB|=2$\sqrt{4-3}$=2,
故选A.
点评 本题考查圆的方程,考查弦长的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
3.已知抛物线C:y2=2px的焦点与圆x2+y2-2x-15=0的圆心重合,则抛物线C的方程是( )
| A. | y2=2x | B. | y2=-2x | C. | y2=4x | D. | y2=-4x |
7.已知函数f(x)=x3+ax2+bx+c有两个极值点x1,x2,若x2<f(x1)<x1,则关于x的方程3(f(x))2+2af(x)+b=0的不同实根个数可能为( )
| A. | 3,4,5 | B. | 4,5,6 | C. | 2,4,5 | D. | 2,3,4 |
1.执行如图所示的程序框图,如果输出T=6,那么判断框内应填入的条件是( )
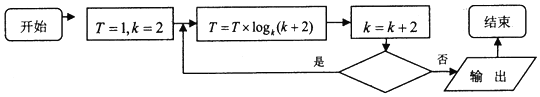
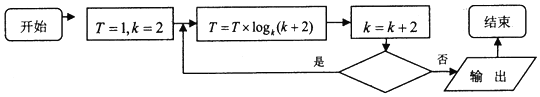
| A. | k<32 | B. | k<33 | C. | k<64 | D. | k<65 |
2.某公司安排6位员工在“元旦(1月1日至1月3日)”假期值班,每天安排2人,每人值班1天,则6位员工中甲不在1日值班的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{6}$ |