题目内容
试判断|a|≥3 是关于x的方程x2+ax+1=0在区间[-1,1]上有解的什么条件?并给出判断理由.
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:由题意知方程在区间上有且只有一个根,由函数零点的存在定理,函数f(x)=x2+ax+1满足f(1)f(5)≤0,由此求得实数a的取值范围,进而结合充要条件的定义,可得答案.
解答:
解:由于方程x2+ax+1=0有解,设它的两个解分别为 x1,x2,则x1•x2=1,
故方程x2+ax+1=0在区间[-1,1]上有唯一解.
设f(x)=x2+ax+1,则有f(-1)f(1)≤0,即 (-a+2)(a+1)≤0,
解得a≤-1,或x≥2,
解|a|≥3得:a≤-3,或a≥3,
∵{a|a≤-3,或x≥3}?{a|a≤-1,或x≥2},
故|a|≥3 是关于x的方程x2+ax+1=0在区间[-1,1]上有解的充分不必要条件.
故方程x2+ax+1=0在区间[-1,1]上有唯一解.
设f(x)=x2+ax+1,则有f(-1)f(1)≤0,即 (-a+2)(a+1)≤0,
解得a≤-1,或x≥2,
解|a|≥3得:a≤-3,或a≥3,
∵{a|a≤-3,或x≥3}?{a|a≤-1,或x≥2},
故|a|≥3 是关于x的方程x2+ax+1=0在区间[-1,1]上有解的充分不必要条件.
点评:本题考查一元二次方程根的分布于系数的关系,如果方程在某区间上有且只有一个根,可根据函数的零点存在定理进行解答,本题解题的关键是对于所给的条件的转化,本题是一个中档题目.

练习册系列答案
相关题目
函数y=log4(1+x2+2x)的图象大致是( )
A、 |
B、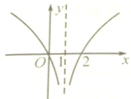 |
C、 |
D、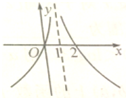 |