题目内容
已知集合
，集合
．
（1）当
时，判断函数
是否属于集合
？并说明理由．若是，则求出区间
；
（2）当时，若函数
，求实数
的取值范围；
（3）当
时，是否存在实数
，当
时，使函数
，若存在，求出的范围，若不存在，说明理由．[来源:]
解： (1)
的定义域是
，
在上是单调增函数．
∴在上的值域是
．由
解得：
故函数属于集合，且这个区间是
． …………5分
(2) 设
，则易知
是定义域
上的增函数．
，
存在区间
，满足
，
．
即方程
在内有两个不等实根． 方程
在内有两个不等实根，令
则其化为:
即
有两个非负的不等实根, 从而有:
； …………10分
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
的左、右焦点分别为
，
是
上的点，
，
，则
B.
C.
D.
，
，
，则（ ）
B 
C 
D 
中，
,且
,点
满足
，则
（ ）
B．
C．
D．
是同一平面内的三个向量，其中
.
，且
，求向量
；
，且
与
垂直，求向量
与向量
的夹角的余弦值.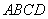
中, 
分别是棱
、
的中点, 则异面直线
所成角的余弦值为（ ）
的一个焦点为（0,3）, 则实数
的值为 . 
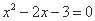,则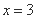
”的逆否命题为:“若
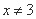,则
”; 
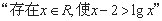的否定是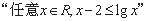
; 
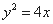上”是“点M的坐标满足方程
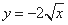”的必要不充分条件; 
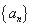是等比数列，则“
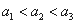”是“数列
（ ）