题目内容
三条直线两两异面,则称为一组“Γ型线”,任选长方体12条面对角线中3条,设“Γ型线”的组数为m,则(
-
)
的展开式中的常数项是( )
| x |
| 2 |
| x |
| m |
| 4 |
| A、-3 | B、-60 |
| C、60 | D、不存在 |
考点:计数原理的应用,二项式系数的性质
专题:
分析:由正方体的几何结构,结合异面直线的定义,按上下底面,前后面,左右面分类讨论,求得m.然后利用二项式定理求出则(
-
)
的展开式,分析可得其常数项,即可得答案.
| x |
| 2 |
| x |
| m |
| 4 |
解答:
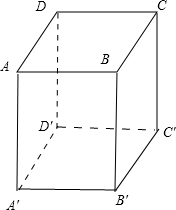 解:如图:在正方体ABCD-A′B′C′D′中,
解:如图:在正方体ABCD-A′B′C′D′中,
上下这组平行平面中,AC、B′D′异面,与其他面的A′D、B′C、DC′、AB′,
可以形成两两异面的直线即“Γ型线”有4组,即AC、B′D′、A′D,AC、B′D′、B′C,AC、B′D′、DC′,AC、B′D′、AB′,
同理:DB与A′C′异面可以确定的“Γ型线”也有4组,
又正方体有三组平行平面,故共有8×3=24组“Γ型线”;即m=24.
则(
-
)
=(
-
)6,
其展开式为Tr+1=C6r(
)6-r×(-
)r=(-2)r×C6r×x3-
,
分析可得,其常数项为T3=(-2)2×C62=60,
故选:C.
 解:如图:在正方体ABCD-A′B′C′D′中,
解:如图:在正方体ABCD-A′B′C′D′中,上下这组平行平面中,AC、B′D′异面,与其他面的A′D、B′C、DC′、AB′,
可以形成两两异面的直线即“Γ型线”有4组,即AC、B′D′、A′D,AC、B′D′、B′C,AC、B′D′、DC′,AC、B′D′、AB′,
同理:DB与A′C′异面可以确定的“Γ型线”也有4组,
又正方体有三组平行平面,故共有8×3=24组“Γ型线”;即m=24.
则(
| x |
| 2 |
| x |
| m |
| 4 |
| x |
| 2 |
| x |
其展开式为Tr+1=C6r(
| x |
| 2 |
| x |
| 3r |
| 2 |
分析可得,其常数项为T3=(-2)2×C62=60,
故选:C.
点评:本题考查简单的计数原理,难点在于合理作图与正确分类讨论,属于难题.

练习册系列答案
相关题目
若函数f(x)=
cos(ωx+φ)对任意x∈R都有f(
-x)=f(
+x),则f(
)的值为( )
| 5 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
A、
| ||
B、-
| ||
C、±
| ||
| D、0 |
下列关于正弦定理的叙述或变形中错误的是( )
| A、在△ABC中,a:b:c=sinA:sinB:sinC | ||||
| B、在△ABC中,a=b?sin2A=sin2B | ||||
C、△ABC中:
| ||||
| D、△ABC中,正弦值较大的角所对的边也较大 |
已知实数a,b满足-1≤a≤1,0≤b≤1,则函数f(x)=x3-ax2+bx无极值的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
如图是一个物体的三视图,则这个物体的形状是( )


| A、圆柱 | B、长方体 |
| C、立方体 | D、圆锥 |
函数f(x)=(1-cos2x)•cos2x的最小正周期是( )
| A、2π | ||
| B、π | ||
C、
| ||
D、
|
函数f(x)=x2+bx在点A(1,f(1))处的切线方程为3x-y-1=0,设数列{
}的前n项和Sn,则S2011为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|