题目内容
6.已知cosα+cosβ=$\frac{1}{2}$,则cos$\frac{α+β}{2}$cos$\frac{α-β}{2}$的值为$\frac{1}{4}$.分析 用三角函数的积化和差公式化简所求后代入已知即可求值.
解答 解:∵cosα+cosβ=$\frac{1}{2}$,
∴cos$\frac{α+β}{2}$cos$\frac{α-β}{2}$=$\frac{1}{2}$[cos($\frac{α+β}{2}$-$\frac{α-β}{2}$)+cos($\frac{α+β}{2}$+$\frac{α-β}{2}$)]=$\frac{1}{2}$(cosα+cosβ)=$\frac{1}{2}×\frac{1}{2}$=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题主要考查了三角函数的积化和差公式在三角函数求值中的应用,属于基础题.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
17.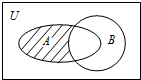 已知全集U=R,集合$A=\{\;x|\;{(\frac{1}{2})^x}≤1\;\}$,B={x|x2-6x+8≤0},则图中阴影部分所表示的集合为( )
已知全集U=R,集合$A=\{\;x|\;{(\frac{1}{2})^x}≤1\;\}$,B={x|x2-6x+8≤0},则图中阴影部分所表示的集合为( )
 已知全集U=R,集合$A=\{\;x|\;{(\frac{1}{2})^x}≤1\;\}$,B={x|x2-6x+8≤0},则图中阴影部分所表示的集合为( )
已知全集U=R,集合$A=\{\;x|\;{(\frac{1}{2})^x}≤1\;\}$,B={x|x2-6x+8≤0},则图中阴影部分所表示的集合为( )| A. | {x|x≤0} | B. | {x|2≤x≤4} | C. | {x|0<x≤2或x≥4} | D. | {x|0≤x<2或x>4} |
1.若y=f(x2),则y′等于( )
| A. | 2xf′(x2) | B. | 2xf′(x) | C. | 4x2f(x) | D. | f′(x2) |