题目内容
10.已知$|\overrightarrow a|=5$,$|\overrightarrow b|=3$,且$\overrightarrow a•\overrightarrow b=-9$,则$\overrightarrow a$在$\overrightarrow b$上的射影的数量为-3.分析 根据射影的定义,得向量$\overrightarrow a$在$\overrightarrow b$上的射影为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$,代值计算即可.
解答 解:$|\overrightarrow a|=5$,$|\overrightarrow b|=3$,且$\overrightarrow a•\overrightarrow b=-9$,根据射影的定义,得向量$\overrightarrow a$在$\overrightarrow b$上的射影为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=$\frac{-9}{3}$=-3,
故答案为:-3.
点评 本题考查了平面向量的应用问题,解题时应根据射影的定义,求出答案来,是基础题.

练习册系列答案
相关题目
1.已知△ABC的顶点B,C在椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$上,顶点A是椭圆的一个焦点,且椭圆的另一个焦点在BC上,则△ABC的周长是( )
| A. | 8 | B. | 8$\sqrt{3}$ | C. | 16 | D. | 24 |
15.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | 8 |
20.执行如图所示的程序图,则输出的S值为( )


| A. | 4 | B. | 3 | C. | -2 | D. | -3 |
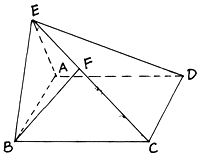 如图,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,点F在CE上,且BF⊥平面ACE;
如图,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,点F在CE上,且BF⊥平面ACE;