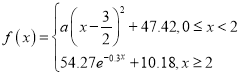题目内容
【题目】设函数![]() 、
、![]() 满足关系
满足关系![]() ,其中
,其中![]() 是常数.
是常数.
(1)设![]() ,
,![]() ,求
,求![]() 的解析式;
的解析式;
(2)是否存在函数![]() 及常数
及常数![]() (
(![]() )使得
)使得![]() 恒成立?若存在,请你设计出函数
恒成立?若存在,请你设计出函数![]() 及常数
及常数![]() ;不存在,请说明理由;
;不存在,请说明理由;
(3)已知![]() 时,总有
时,总有![]() 成立,设函数
成立,设函数![]() (
(![]() )且
)且![]() ,对任意
,对任意![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(3)
;(3)![]() .
.
【解析】
(1)由f(x)的解析式求出f(x+α)的解析式,相乘后得到函数g(x)的解析式;
(2)由逆向思维可知f(x)f(x+α)=sinxcosx,由此可得函数f(x)及一个α;
(3)由给出的f(x)求出g(x),从而求出sin[g(x)]与g(sinx),借助于![]() 可得答案.
可得答案.
(1)∵f(x)=cosx+sinx,![]()
∴f(x+α)=cosx﹣sinx;
∴g(x)=f(x)f(x+α)=(cosx+sinx)(cosx﹣sinx)
=cos2x﹣sin2x=cos2x;
(2)∵g(x)![]() sin2x=2sinxcosx,
sin2x=2sinxcosx,
若f(x)=![]() sinx,则f(x+α)=
sinx,则f(x+α)=![]() sin(x+α)=
sin(x+α)=![]() cosx
cosx![]()
∴f(x)=![]() sinx,常数
sinx,常数![]() ;
;
也可以设f(x)=![]() cosx,则f(x+α)=
cosx,则f(x+α)=![]() cos(x+α)=
cos(x+α)=![]() sinx
sinx![]()
∴f(x)=![]() cosx,常数
cosx,常数![]() ;
;
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
(3)由题意g(x)=kx,sin[g(x)]=sinkx,g(sinx)=ksinx
又0<k<1,所以![]() ,
,
则![]() ,所以sinkx>ksinx,
,所以sinkx>ksinx,
即sin[g(x)]>g(sinx).

【题目】某企业为提高生产质量,引入了一批新的生产设备,为了解生产情况,随机抽取了新、旧设备生产的共200件产品进行质量检测,统计得到产品的质量指标值如下表及图(所有产品质量指标值均位于区间![]() 内),若质量指标值大于30,则说明该产品质量高,否则说明该产品质量一般.
内),若质量指标值大于30,则说明该产品质量高,否则说明该产品质量一般.
质量指标 | 频数 |
| 2 |
| 8 |
| 10 |
| 30 |
| 20 |
| 10 |
合计 | 80 |
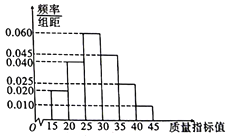
(1)根据上述图表完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为产品质量高与引人新设备有关;
的把握认为产品质量高与引人新设备有关;
新旧设备产品质量![]() 列联表
列联表
产品质量高 | 产品质量一般 | 合计 | |
新设备产品 | |||
旧设备产品 | |||
合计 |
(2)从旧设备生产的质量指标值位于区间![]() 的产品中,按分层抽样抽取6件产品,再从这6件产品中随机选取2件产品进行质量检测,求至少有一件产品质量指标值位于
的产品中,按分层抽样抽取6件产品,再从这6件产品中随机选取2件产品进行质量检测,求至少有一件产品质量指标值位于![]() 的概率.
的概率.
附: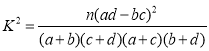 ,
,![]() .
.
| 0.10 | 0.05 | 0.01 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |