题目内容
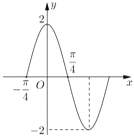
【题目】如图是函数![]() 一个周期内的图象,将
一个周期内的图象,将![]() 图象上所有点的横坐标伸长为原来的2倍,纵坐标不变,再把所得图象向右平移
图象上所有点的横坐标伸长为原来的2倍,纵坐标不变,再把所得图象向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象.
的图象.
(1)求函数![]() 和
和![]() 的解析式;
的解析式;
(2)若![]() ,求
,求![]() 的所有可能的值;
的所有可能的值;
(3)求函数![]() (
(![]() 为正常数)在区间
为正常数)在区间![]() 内的所有零点之和.
内的所有零点之和.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或1;(3)当
或1;(3)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,171
时,171![]() .
.
【解析】
(1)由三角函数图象求得![]() ,
,![]() ,
,![]() ,再由三角函数图象的平移可得
,再由三角函数图象的平移可得![]() ;
;
(2)由![]() ,解得
,解得![]() 或
或![]() ,再求解
,再求解![]() 即可;
即可;
(3)先解得![]() ,再讨论
,再讨论![]() 与1的大小关系,再解三角方程,结合正弦函数图象的对称性求各零点之和即可.
与1的大小关系,再解三角方程,结合正弦函数图象的对称性求各零点之和即可.
解:(1)由图可知![]() ,
,![]() ,即
,即![]() ,即
,即![]() ,
,
则![]() ,又
,又![]() ,又
,又![]() ,所以
,所以![]() ,
,
故![]() ,
,
将![]() 的图象上所有点的横坐标伸长为原来的2倍,纵坐标不变,得函数解析式为
的图象上所有点的横坐标伸长为原来的2倍,纵坐标不变,得函数解析式为![]() ,再把所得图象向右平移
,再把所得图象向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则
的图象,则![]() ,
,
即![]() ,
,![]() ;
;
(2)当![]() ,即
,即![]() ,解得
,解得![]() 即
即![]() 或
或![]() ,即
,即![]() 或
或![]() 或
或![]() (
(![]() )
)
当![]() 时,所以
时,所以![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
故![]() 的所有可能的值为
的所有可能的值为![]() 或1;
或1;
(3)令![]() ,即
,即![]() ,即
,即![]() ,
,
解得![]() ,又因为
,又因为![]() ,又
,又![]() ,所以
,所以 ![]() ,
,
当![]() 时,由函数
时,由函数![]() 的对称轴方程可得
的对称轴方程可得![]() 在
在![]() ,(
,(![]() )有两个解,且两解之和
)有两个解,且两解之和![]() ,
,
则在![]() 的根之和为
的根之和为![]() ,
,
当 ![]() ,即
,即![]() 时,方程
时,方程![]() 无解,
无解,
当 ![]() ,即
,即![]() 时,方程
时,方程![]() 的解为
的解为![]() ,(
,(![]() ),则在
),则在![]() 的根之和为
的根之和为![]() ,
,
当 ![]() ,即
,即![]() 时,方程
时,方程![]() 在
在![]() ,(
,(![]() )有两个解,且两解之和
)有两个解,且两解之和![]() ,
,
则在![]() 的根之和为
的根之和为![]() ,
,
综上可得:当![]() 时,函数
时,函数![]() 在区间
在区间![]() 内的所有零点之和为
内的所有零点之和为![]() .
.
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 内的所有零点之和为
内的所有零点之和为![]() .
.
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 内的所有零点之和为
内的所有零点之和为![]() .
.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目