题目内容
12．已知{an}是递增数列，对于任意的正整数n均有an=n2+λn恒成立，则实数λ的取值范围是（ ）| A． | [-2，+∞） | B． | （-3，+∞） | C． | R | D． | ∅ |
分析 {an}是递增数列，对于任意的正整数n均有an=n2+λn恒成立，可得an+1＞an，解出即可．
解答 解：∵{an}是递增数列，对于任意的正整数n均有an=n2+λn恒成立，
∴an+1＞an，
∴（n+1）2+λ（n+1）＞n2+λn，
化为λ＞-（2n+1），
∴λ＞-3．
则实数λ的取值范围是（-3，+∞）．
故选：B．
点评 本题考查了数列的单调性，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
17．
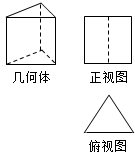如图，水平放置的三棱柱的侧棱长和底边长均为4，且侧棱垂直于底面，正视图是边长为4的正方形，则三棱柱的左视图面积为（ ）
如图，水平放置的三棱柱的侧棱长和底边长均为4，且侧棱垂直于底面，正视图是边长为4的正方形，则三棱柱的左视图面积为（ ）| A． | 8$\sqrt{3}$ | B． | 2$\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 4$\sqrt{3}$ |
4．
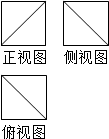将某正方体工件进行切削，把它加工成一个体积尽可能大的新工件，新工件的三视图如图所示，则原工件材料的利用率为〔材料的利用率=$\frac{新工件的体积}{原工件的体积}$〕（ ）
将某正方体工件进行切削，把它加工成一个体积尽可能大的新工件，新工件的三视图如图所示，则原工件材料的利用率为〔材料的利用率=$\frac{新工件的体积}{原工件的体积}$〕（ ）| A． | $\frac{7}{8}$ | B． | $\frac{6}{7}$ | C． | $\frac{5}{6}$ | D． | $\frac{4}{5}$ |
1．已知f（x）+f（-x）=8，f（lg（log210））=5，则f（lg（lg2））=（ ）
| A． | -5 | B． | -1 | C． | 3 | D． | 4 |
2．已知幂函数f（x）的图象过点$（4，\frac{1}{2}）$，则f（16）的值是（ ）
| A． | $\frac{1}{4}$ | B． | $4\sqrt{2}$ | C． | $\frac{{\sqrt{2}}}{4}$ | D． | 64 |