题目内容
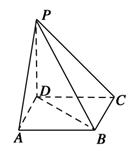
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(1) 证明PA⊥BD;
(2) 设PD=AD=1,求棱锥D-PBC的高.
 |
(1)证明:因为∠DAB=60°,AB=2AD,由余弦定理得BD= AD.
AD.
从而BD2+AD2=AB2,故BD⊥AD.又PD⊥底面ABCD,可得BD⊥PD.
所以BD⊥平面PAD.故PA⊥BD.
(2)如图,作DE⊥PB,垂足为E.已知PD⊥底面ABCD,则PD⊥BC.由(1)知BD⊥AD,
又BC∥AD,所以BC⊥BD.故BC⊥平面PBD,所以BC⊥DE.则DE⊥平面PBC.
由题设知PD=1,则BD= ,PB=2.根据DE·PB=PD·BD,得DE=
,PB=2.根据DE·PB=PD·BD,得DE= ,
,
即棱锥D-PBC的高为 .
.


练习册系列答案
相关题目
 B.
B. C.
C. D.
D.
 的最小值为
的最小值为 +2 B.
+2 B.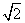 ,
,
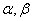 为平面,且m
为平面,且m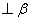 ,则“m//
,则“m//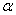 ”是“
”是“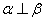 ”的充要条件;
”的充要条件;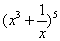 的展开式中含x3的项的系数为60;
的展开式中含x3的项的系数为60;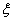 ~N(0,1),若P(
~N(0,1),若P(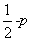 ;
;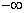 ,2);
,2);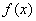 满足
满足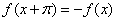 ,且0<x<
,且0<x<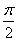 时
时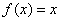 ,则函数
,则函数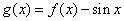 在[
在[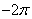 ,
,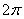 ]上有5个零点.
]上有5个零点. ”的单调递增函数是( )
”的单调递增函数是( ) B.
B. C.
C. D.
D.
 ,则图中阴影部分表示的集合为( )
,则图中阴影部分表示的集合为( ) A.
A. B.
B.
 D.
D.