题目内容
17.已知曲线C1的参数方程为$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.{\;}_{\;}^{\;}$(t为参数),曲线C2的参数方程为 $\left\{\begin{array}{l}x=cosθ\\ y=sinθ\end{array}$(θ为参数).(1)若C1与C2相交于A、B两点,求|AB|;
(2)若把曲线C2上各点的横坐标扩大到原来的2倍,纵坐标保持不变,得到曲线C3,设点P是曲线C3上的一个动点,求它到曲线C1的距离的最大值.
分析 (1)将$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$代入x2+y2=1得t2+t=0,利用参数的意义求|AB|;
(2)求出曲线C3,利用参数方程,点到直线的距离公式,即可求它到曲线C1的距离的最大值.
解答 解:(1)将$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$代入x2+y2=1得t2+t=0,∴|AB|=|t1-t2|=1
(2)C1:y=$\sqrt{3}$(x-1),C2:x2+y2=1;C3:$\frac{{x}^{2}}{4}+{y}^{2}$=1,
因此设$P(2cosα,sinα)⇒d=\frac{{|{2\sqrt{3}cosα-sinα-\sqrt{3}}|}}{2}=\frac{{|{\sqrt{13}sin(α+β)-\sqrt{3}}|}}{2}$
因此${d_{max}}=\frac{{\sqrt{13}+\sqrt{3}}}{2}$.
点评 本题考查参数方程的运用,考查参数的运用,考查点到直线距离公式的运用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.下列函数中,周期是π,又是偶函数的是( )
| A. | y=sinx | B. | y=cosx | C. | y=sin2x | D. | y=cos2x |
5.空间几何体的三视图如图所示,则该几何体的体积为( )
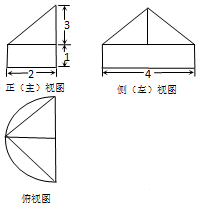

| A. | 4+2π | B. | 12+2π | C. | 4+4π | D. | 12+4π |
9.一个几何体的三视图如图所示,则这个几何体外接球体积与该几何体的体积比为( )


| A. | $\frac{3\sqrt{3}}{2}$π | B. | $\frac{\sqrt{3}}{4}$π | C. | $\frac{3\sqrt{3}}{4}$π | D. | $\frac{\sqrt{3}}{8}$π |
6.若一个正六棱柱(底面是正六边形,侧棱垂直于底面)的正视图如图所示,则其体积等于( )

| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{3\sqrt{3}}{2}$ | C. | 2$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
 ,则A等于 .
,则A等于 .