题目内容
设数列{an}的前n项和为Sn,已知Sn=2an-2n+1(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=log
2,数列{bn}的前n项和为Bn,若存在整数m,使对任意n∈N*且n≥2,都有B3n-Bn>
成立,求m的最大值m0;
(3)对任意n∈N*,都有1+
+
+…+
<
.
(1)求数列{an}的通项公式;
(2)设bn=log
| an |
| n+1 |
| m |
| 20 |
(3)对任意n∈N*,都有1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| m0 |
| 9 |
考点:数列的求和,数列的函数特性
专题:等差数列与等比数列
分析:(1)由Sn=2an-2n+1(n∈N*)可得当n≥2时,an=Sn-Sn-1,化为
-
=1,利用等差数列的通项公式即可得出.
(2)由bn=log
2=log2n2=
,可得B3n-Bn=
+
+…+
,令f(n)=
+
+…+
,可证明数列{f(n)}为单调递增数列.当n≥2时,f(n)的最小值为f(2)=
+
+
+
=
.由
<
,m为整数,可得m的最大值为18.
(3)由(2)可知:
=2,当n=1时,1<2成立.当n≥2时,1+
+
+…+
<1+
+
+…+
=1+1-
即可证明.
| an |
| 2n |
| an-1 |
| 2n-1 |
(2)由bn=log
| an |
| n+1 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+2n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+2n |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 19 |
| 20 |
| m |
| 20 |
| 19 |
| 20 |
(3)由(2)可知:
| m0 |
| 9 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| (n-1)×n |
| 1 |
| n |
解答:
(1)解:∵Sn=2an-2n+1(n∈N*).
∴当n≥2时,an=Sn-Sn-1=2an-2n+1-(2an-1-2n),化为
-
=1,
∴数列{
}是等差数列,
当n=1时,a1=S1=2a1-22,解得a1=4.
∴
=2+(n-1)×1=n+1,
∴an=(n+1)•2n.
(2)解:∵bn=log
2=log2n2=
,
∴B3n-Bn=
+
+…+
,
令f(n)=
+
+…+
,
则f(n+1)=
+
+…+
+
+
+
,
∴f(n+1)-f(n)=
+
+
-
>
+
-
=0,
∴数列{f(n)}为单调递增数列.
∴当n≥2时,f(n)的最小值为f(2)=
+
+
+
=
.
由
<
,m为整数,∴m的最大值为18.
(3)证明:由(2)可知:
=2,当n=1时,1<2成立.
当n≥2时,1+
+
+…+
<1+
+
+…+
=1+1-
<
=2成立.
∴当n≥2时,an=Sn-Sn-1=2an-2n+1-(2an-1-2n),化为
| an |
| 2n |
| an-1 |
| 2n-1 |
∴数列{
| an |
| 2n |
当n=1时,a1=S1=2a1-22,解得a1=4.
∴
| an |
| 2n |
∴an=(n+1)•2n.
(2)解:∵bn=log
| an |
| n+1 |
| 1 |
| n |
∴B3n-Bn=
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+2n |
令f(n)=
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+2n |
则f(n+1)=
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 3n |
| 1 |
| 3n+1 |
| 1 |
| 3n+2 |
| 1 |
| 3n+3 |
∴f(n+1)-f(n)=
| 1 |
| 3n+1 |
| 1 |
| 3n+2 |
| 1 |
| 3n+3 |
| 1 |
| n+1 |
| 1 |
| 3n+3 |
| 1 |
| 3n+3 |
| 2 |
| 3n+3 |
∴数列{f(n)}为单调递增数列.
∴当n≥2时,f(n)的最小值为f(2)=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 19 |
| 20 |
由
| m |
| 20 |
| 19 |
| 20 |
(3)证明:由(2)可知:
| m0 |
| 9 |
当n≥2时,1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| (n-1)×n |
| 1 |
| n |
| m0 |
| 9 |
点评:本题考查了等差数列的通项公式、对数的运算性质、“裂项求和”、数列的单调性,考查了放缩法证明不等式,考查了推理能力与计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都是1,且夹角都是60°,则相对的面AD1与面BC1的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
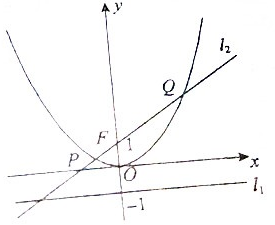 已知动圆C过定点F(0,1),且与直线l1:y=-1相切,圆心C的轨迹为E.
已知动圆C过定点F(0,1),且与直线l1:y=-1相切,圆心C的轨迹为E. 已知正三棱锥V-ABC的正视图、侧视图和俯视图如图所示.
已知正三棱锥V-ABC的正视图、侧视图和俯视图如图所示.