题目内容
“过点(0,1)的直线l与双曲线x2-
=1有且仅有一个公共点”是“直线l的斜率k的值为±2”的( )
| y2 |
| 3 |
| A、充分必要条件 |
| B、充分但不必要条件 |
| C、必要但不充分条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:圆锥曲线的定义、性质与方程,简易逻辑
分析:根据直线和双曲线的位置关系,利用充分条件和必要条件的定义即可得到结论.
解答:
解:设过(0,1)的直线斜率为k,则对应的直线方程为:y-1=kx,即y=kx+1,
代入双曲线方程x2-
=1得x2-
(kx+1)2=1,
整理得(3-k2)x2-2kx-4=0,
当3-k2=0,即k=±
时,方程有一个公共点,此时直线与双曲线的渐近线平行,
当3-k2≠0,要使直线l与双曲线x2-
=1有且仅有一个公共点,
则△=4k2+16(3-k2)=0,
即k2=4,解得k=±2,
即过点(0,1)的直线l与双曲线x2-
=1有且仅有一个公共点”时,k=±2或k=±
,
∴“过点(0,1)的直线l与双曲线x2-y2=
有且仅有一个公共点”是“直线l的斜率k的值为±2”的必要不充分条件,
故选:C.
代入双曲线方程x2-
| y2 |
| 3 |
| 1 |
| 3 |
整理得(3-k2)x2-2kx-4=0,
当3-k2=0,即k=±
| 3 |
当3-k2≠0,要使直线l与双曲线x2-
| y2 |
| 3 |
则△=4k2+16(3-k2)=0,
即k2=4,解得k=±2,
即过点(0,1)的直线l与双曲线x2-
| y2 |
| 3 |
| 3 |
∴“过点(0,1)的直线l与双曲线x2-y2=
| 1 |
| 3 |
故选:C.
点评:本题主要考查充分条件和必要条件的判断,利用不等式之间的关系是解决本题的关键.

练习册系列答案
相关题目
“m>0”是“方程
+
=1表示椭圆”的( )
| x2 |
| 2 |
| y2 |
| m |
| A、充分不必要条件 |
| B、充要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
均值都是5的四组数据条形图如下,将四组数据作比较,错误的是( )
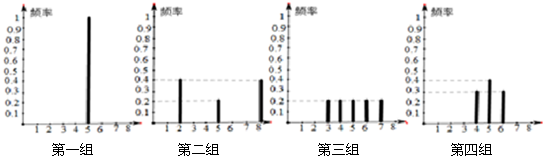

| A、第一组标准差最小 |
| B、第二组极差最大 |
| C、第三组最稳定 |
| D、第三组的方差大于第四组的方差 |
按如图所示的程序框图运行后,输出的结果是63,则判断框中的整数M的值是( )


| A、5 | B、6 | C、7 | D、8 |
直线l经过坐标原点和点(-1,-1),则直线l的倾斜角是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
设集合A={x||x|≤2},B={y|y=x2},则A∩B=( )
| A、[-2,2] |
| B、[0,2] |
| C、(0,2] |
| D、[0,+∞) |