题目内容
已知数列{an}中,an=
,则a9= (用数字作答),设数列{an}的前n项和为Sn,则S9= (用数字作答).
|
考点:数列的求和
专题:等差数列与等比数列
分析:由已知条件得到a9=29-1,由此能求出a9的值.再由an=
,分别求出前9项的值并相加,利用分组求和法能求出S9.
|
解答:
解:∵数列{an}中,an=
,
∴a9=29-1=28=256.
S9=21-1+(2×2-1)+23-1+(2×4-1)+25-1+(2×6-1)+27-1+(2×8-1)+29-1
=(20+22+24+26+28)+2(2+4+6+8)-1×4
=
+2×
(2+8)-4
=
+40-4
=341+36
=377.
故答案为:256,377.
|
∴a9=29-1=28=256.
S9=21-1+(2×2-1)+23-1+(2×4-1)+25-1+(2×6-1)+27-1+(2×8-1)+29-1
=(20+22+24+26+28)+2(2+4+6+8)-1×4
=
| 1-45 |
| 1-4 |
| 4 |
| 2 |
=
| 45-1 |
| 3 |
=341+36
=377.
故答案为:256,377.
点评:本题考查数列的第9项和前9项和的值的求法,是中档题,解题时要注意递推思想和分组求和法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知等差数列{an}的前3项分别为4、6、8,则数列{an}的第4项为( )
| A、7 | B、8 | C、10 | D、12 |
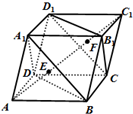 已知平行六面体ABCD-A1B1C1D1,AC1与平面A1BD,CB1D1交于E,F两点.给出以下命题,其中真命题有
已知平行六面体ABCD-A1B1C1D1,AC1与平面A1BD,CB1D1交于E,F两点.给出以下命题,其中真命题有