题目内容

已知2a=3b=6c，则
a+b
c
的取值范围为（　　）
A、（2，3）
B、（3，4）
C、（4，5）
D、（5，6）
考点：对数的运算性质
专题：函数的性质及应用
分析：设2a=3b=6c=k＞0，可得a=
lgk
lg2
，b=
lgk
lg3
，c=
lgk
lg6
.
a+b
c
=
lg26
lg2lg3
，再利用基本不等式的性质、对数函数的单调性即可得出．
解答： 解：设2a=3b=6c=k＞0
∴a=
lgk
lg2
，b=
lgk
lg3
，c=
lgk
lg6
．
则
a+b
c
=
lgk
lg2
+
lgk
lg3
lgk
lg6
=
lg26
lg2lg3
＞
lg26
(
lg2+lg3
2
)2
=4，
另一方面
a+b
c
=
lg26
lg2lg3
=
(lg2+lg3)2
lg2lg3
=
lg2
lg3
+2+
lg3
lg2
＜1+2+2=5，
∴
a+b
c
∈（4，5）．
故选：C．
点评：本题考查了基本不等式的性质、对数函数的单调性、对数的换底公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
已知{an}是正项数列，a1=1，且点（
an
，an+1）（n∈N*）在函数y=x2+1的图象上．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=1+
1
anan+1
，求数列{bn}的前n项和Sn．
已知函数f（x）=3x+4，求函数f-1（x+1）的解析式
 
．
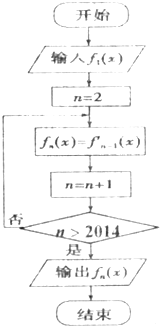在如图所示的程序框图中，当n∈N*（n＞1）时，函数fn（x）等于函数fn-1（x）的导函数，若输入函数f1（x）=sinx+cosx，则输出的函数fn（x）可化为（　　）
A、
2
sin（x+
π
4
）
B、
2
sin（x-
π
4
）
C、-
2
sin（x-
π
4
）
D、-
2
sin（x+
π
4
）
角α（0≤α≤2π）的终边过点P（sin
3
5
π，cos
3
5
π），则α=
 
．
与函数y=x为相同函数的是（　　）
A、y=
x2
B、y=
x2
x
C、y=elnx
D、y=log22x
已知点A（-
3
，1），点B在y轴上，直线AB的倾斜角为
2π
3
，求点B的坐标．
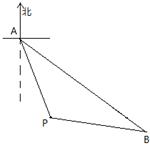如图，某船在A处看见灯塔P在南偏东15°方向，后来船沿南偏东45°的方向航行30km后，到达B处，看见灯塔P在船的西偏北15°方向，则这时船与灯塔的距离是（　　）
A、10km
B、20km
C、10
3
km
D、5
3
km
（函数的定义域）函数y=log2（1+x）+
4-2x
的定义域为（　　）
A、（-1，2）
B、（0，2]
C、（0，2）
D、（-1，2]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网