题目内容
3. 如图,四面体ABCD中,AB=DC=1,BD=$\sqrt{2}$,AD=BC=$\sqrt{3}$,二面角A-BD-C的平面角的大小为60°,E,F分别是BC,AD的中点,则异面直线EF与AC所成的角的余弦值是( )
如图,四面体ABCD中,AB=DC=1,BD=$\sqrt{2}$,AD=BC=$\sqrt{3}$,二面角A-BD-C的平面角的大小为60°,E,F分别是BC,AD的中点,则异面直线EF与AC所成的角的余弦值是( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
分析 由已知得∠ABO=∠BDC=90°,<$\overrightarrow{BA},\overrightarrow{DC}$>=60°,$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{DC}$,从而得到|$\overrightarrow{AC}$|=$\sqrt{3}$,取BD中点H,CD中点G,连结FH、EH、GE、GF、EF,则∠EFG是异面直线EF与AC所成的角,由此能求出异面直线EF与AC所成的角的余弦值.
解答  解:∵四面体ABCD中,AB=DC=1,BD=$\sqrt{2}$,AD=BC=$\sqrt{3}$
解:∵四面体ABCD中,AB=DC=1,BD=$\sqrt{2}$,AD=BC=$\sqrt{3}$
二面角A-BD-C的平面角的大小为60°,E,F分别是BC,AD的中点,
∴AB2+BD2=AD2,BD2+CD2=BC2,
∴∠ABO=∠BDC=90°,<$\overrightarrow{BA},\overrightarrow{DC}$>=60°,
$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{DC}$,
∴${\overrightarrow{AC}}^{2}$=($\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{DC}$)2=1+2+1+2×1×1×cos120°=3,∴|$\overrightarrow{AC}$|=$\sqrt{3}$,
取BD中点H,CD中点G,连结FH、EH、GE、GF、EF,
得∠FHE=60°,HF=HE=$\frac{1}{2}$,∴△HEF是正三角形,∴EF=$\frac{1}{2}$,
由三角形中位线定理得GF∥AC,∴∠EFG是异面直线EF与AC所成的角,
∵$GF=\frac{1}{2}AC=\frac{\sqrt{3}}{2}$,$GE=\frac{1}{2}BD=\frac{\sqrt{2}}{2}$,EF=$\frac{1}{2}$,
∴∠FEG=90°,
∴cos$∠EFG=\frac{EF}{FG}$=$\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}=\frac{\sqrt{3}}{3}$,
∴异面直线EF与AC所成的角的余弦值是$\frac{\sqrt{3}}{3}$.
故选:B.
点评 本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意三角形中位线定理、勾股定理、余弦定理、向量性质的合理运用.

| A. | $\sqrt{2}$ | B. | $\sqrt{2}$+1 | C. | $\sqrt{5}$ | D. | $\sqrt{5}$-1 |
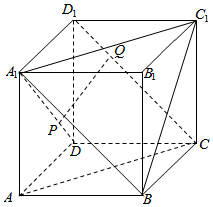
| A. | 在CD1上存在点Q,使得PQ∥平面AA1C1C | |
| B. | 在CD1上存在点Q,使得PQ⊥平面AA1C1C | |
| C. | 在CD1上存在点Q,使得PQ∥平面A1BC1 | |
| D. | 在CD1上存在点Q,使得PQ⊥平面A1BC1 |