题目内容
6.已知单位向量$\overrightarrow{a}$和$\overrightarrow{b}$,若$\overrightarrow{a}$$•\overrightarrow{b}$=$\frac{1}{2}$,且|$\overrightarrow{c}$$-\overrightarrow{a}$|+$\overrightarrow{c}$$-2\overrightarrow{b}$|=$\sqrt{3}$,则|$\overrightarrow{c}$$+2\overrightarrow{a}$|的取值范围是[1,2].分析 由题意将所用的向量放到坐标系中用坐标表示,借助于两点之间的距离公式以及几何意义,即可得到最值.
解答 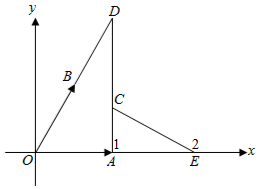 解:∵$\overrightarrow{a}•\overrightarrow{b}=\frac{1}{2}$,$|\overrightarrow{a}|=|\overrightarrow{b}|=1$,
解:∵$\overrightarrow{a}•\overrightarrow{b}=\frac{1}{2}$,$|\overrightarrow{a}|=|\overrightarrow{b}|=1$,
∴$\overrightarrow{a},\overrightarrow{b}$的夹角为60°.
设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$,A(1,0),B($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),C(x,y).
∵|$\overrightarrow{c}$$-\overrightarrow{a}$|+$\overrightarrow{c}$$-2\overrightarrow{b}$|=$\sqrt{3}$,
∴$\sqrt{(x-1)^{2}+{y}^{2}}$+$\sqrt{(x-1)^{2}+(y-\sqrt{3})^{2}}$=$\sqrt{3}$.
∴C点到A(1,0)与到点D(1,$\sqrt{3}$)的距离之和为$\sqrt{3}$,
∵|AD|=$\sqrt{3}$,
∴C在线段AD上.
而|$\overrightarrow{c}$$+2\overrightarrow{a}$|=$\sqrt{(x-2)^{2}+{y}^{2}}$,表示C(x,y)到点E(2,0)的距离.
∴当C位于点A时,|CE|取得最小值1,当C位于D时,|CE|取得最大值2.
故答案为:[1,2].
点评 本题考查了向量的坐标运算、两点之间的距离公式,关键是利用几何意义和坐标法解决.

| A. | (-2,3) | B. | (1,2) | C. | (2,3) | D. | (2,4) |
| A. | a+bi=a-bi | B. | a+bi=-a+bi | C. | ab=0 | D. | a=b=0 |
| A. | (2,4) | B. | [2,4] | C. | [2,4) | D. | [$\sqrt{5}$,4) |