题目内容
15.已知△ABC的内角A,B,C的对边分别为a,b,c,且acosC+csinA-b=0.(I)求角A的大小;
(Ⅱ)若a=3,求△ABC的面积的最大值.
分析 (I)根据正弦定理以及两角和差的正弦公式进行化简即可求角A的大小;
(Ⅱ)利用余弦定理、基本不等式的性质、三角形的面积计算公式即可得出.
解答 解:(I)∵acosC+csinA-b=0,
∴由正弦定理得sinAcosC+sinCsinA=sinB,
即sinAcosC+sinCsinA=sin(A+C)=sinAcosC+cosAsinC,
即sinCsinA=cosAsinC,
∵sinC≠0,
∴sinA=cosA,即tanA=1,
则A=$\frac{π}{4}$;
(Ⅱ)∵A=$\frac{π}{4}$,a=3;
∴由余弦定理可得:a2=b2+c2-2bccosA,
∴9=b2+c2-2bccosA≥2bc-$\sqrt{2}$bc=(2-$\sqrt{2}$)bc,
∴bc≤$\frac{9}{2-\sqrt{2}}$,当且仅当b=c时取等号.
∴∴S△ABC=$\frac{1}{2}$bcsinA≤$\frac{1}{2}$×$\frac{9}{2-\sqrt{2}}$×$\frac{\sqrt{2}}{2}$=$\frac{9(1+\sqrt{2})}{4}$.
∴△ABC的面积的最大值是$\frac{9(1+\sqrt{2})}{4}$.
点评 本题考查了余弦定理、基本不等式的性质、三角形的面积计算公式,考查了推理能力和计算能力,利用两角和差的正弦公式进行化简是解决本题的关键.

练习册系列答案
相关题目
5. 如图,在四边形ABCD中,∠B=120°,∠C=150°,且AB=3,BC=1,CD=2,则AD的长所在的区间为( )
如图,在四边形ABCD中,∠B=120°,∠C=150°,且AB=3,BC=1,CD=2,则AD的长所在的区间为( )
 如图,在四边形ABCD中,∠B=120°,∠C=150°,且AB=3,BC=1,CD=2,则AD的长所在的区间为( )
如图,在四边形ABCD中,∠B=120°,∠C=150°,且AB=3,BC=1,CD=2,则AD的长所在的区间为( )| A. | (2,3) | B. | (3,4) | C. | (4,5) | D. | (5,6) |
3.若圆C:x2+y2-4x+4y+m=与x轴交于A、B两点,且∠ACB=120°,则实数m的值为( )
| A. | 24 | B. | -8 | C. | 8 | D. | 4 |
10.一个圆锥底面半径为r,轴截面是直角三角形,则其母线长为( )
| A. | r | B. | 2r | C. | $\frac{\sqrt{2}}{2}$r | D. | $\sqrt{2}$r |
12.在区间[0,π]上随机地取一个数x,则事件“sinx≤$\frac{1}{2}$”发生的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
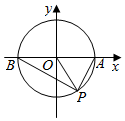 如图,在平面直角坐标系xOy中,单位圆与x轴的正半轴与负半轴分别交于点A,B,角α的始边为OA,终边与单位圆交于x轴下方一点P.
如图,在平面直角坐标系xOy中,单位圆与x轴的正半轴与负半轴分别交于点A,B,角α的始边为OA,终边与单位圆交于x轴下方一点P.


