题目内容
在△ABC中，已知1+
=
，
（1）求角A的大小；
（2）当sinC=3sinB时，求tan（B-
）的值．
| tanA |
| tanB |
| 2sinC |
| sinB |
（1）求角A的大小；
（2）当sinC=3sinB时，求tan（B-
| π |
| 3 |
考点：两角和与差的正切函数
专题：三角函数的求值
分析：（1）由条件根据同角三角函数的基本关系，求得cosA的值，可得A的值．
（2）当sinC=3sinB时，sin（
-B）=3sinB，求得tanB得知，可得tan（B-
）=
得知．
（2）当sinC=3sinB时，sin（
| 2π |
| 3 |
| π |
| 3 |
tanB-tan
| ||
1+tanBtan
|
解答：
解：（1）△ABC中，已知1+
=
，即 1+
=
，即
=
，
求得cosA=
，∴A=
．
（2）当sinC=3sinB时，sin（
-B）=3sinB，即sin
cosB-cos
sinB=3sinB，即
cosB=
sinB，
求得tanB=
，
∴tan（B-
）=
=-
．
| tanA |
| tanB |
| 2sinC |
| sinB |
| sinAcosB |
| cosAsinB |
| 2sinC |
| sinB |
| sinAcosB+cosAsinB |
| sinBcosA |
| 2sinC |
| sinB |
求得cosA=
| 1 |
| 2 |
| π |
| 3 |
（2）当sinC=3sinB时，sin（
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| ||
| 2 |
| 5 |
| 2 |
求得tanB=
| ||
| 5 |
∴tan（B-
| π |
| 3 |
tanB-tan
| ||
1+tanBtan
|
| ||
| 2 |
点评：本题主要考查同角三角函数的基本关系，两角和差的正切公式，属于基础题．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知i是虚数单位，复数z1=1+2i，z2=3+4i，那么z1+z2=（ ）
| A、5+5i | B、4+6i |
| C、10i | D、10 |
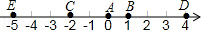如图，A点的初始位置位于数轴上的原点，现对A点做如下移动：第1次从原点向右移动1个单位长度至B点，第2次从B点向左移动3个单位长度至C点，第3次从C点向右移动6个单位长度至D点，第4次从D点向左移动9个单位长度至E点，…，依此类推，这样移动解答：
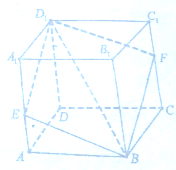如图，在棱长为1的正方体ABCD-A1B1C1D1中，过对角线BD1的平面分别交AA1，CC1于点E，F．