题目内容
19．已知菱形ABCD的边长为a，∠ABC=60°，则$\overrightarrow{BD}$•$\overrightarrow{CD}$=$\frac{3}{2}{a}^{2}$．分析 求出BD及两向量夹角，代入向量的数量积公式计算．
解答 
解：∵菱形ABCD的边长为a，∠ABC=60°，
∴∠BCD=120°，∠BDC=30°，
BD=$\sqrt{{a}^{2}+{a}^{2}-2{a}^{2}cos120°}$=$\sqrt{3}a$．
∴$\overrightarrow{BD}•\overrightarrow{CD}$=$\sqrt{3}a•a•cos30°$=$\frac{3}{2}{a}^{2}$．
点评 本题考查了平面向量的数量积运算，属于基础题．
练习册系列答案
计算高手系列答案
相关题目
19．函数y=sin（x-$\frac{π}{3}$）的单调递增区间是（ ）
| A． | [kπ-$\frac{π}{12}$，kπ+$\frac{5π}{12}$]，k∈Z | B． | [2kπ-$\frac{π}{12}$，2kπ+$\frac{5π}{12}$]，k∈Z | ||
| C． | [kπ-$\frac{π}{6}$，kπ+$\frac{5π}{6}$]，k∈Z | D． | [2kπ-$\frac{π}{6}$，2kπ+$\frac{5π}{6}$]，k∈Z |
10．不等式|x-2|＜2的解集是（ ）
| A． | （-1，1） | B． | （-2，2） | C． | （-1，0）∪（0，1） | D． | （0，4 ） |
7．为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老人，结果如表：
由${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$算得，K2≈9.967
附表：
参照附表，得到的正确结论是（ ）
| 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
附表：
| P（K2≥k） | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A． | 有99%以上的把握认为“需要志愿者提供帮助与性别无关” | |
| B． | 有99%以上的把握认为“需要志愿者提供帮助与性别有关” | |
| C． | 在犯错误的概率不超过0.1%的前提下，认为“需要志愿者提供帮助与性别有关” | |
| D． | 在犯错误的概率不超过0.1%的前提下，认为“需要志愿者提供帮助与性别无关” |
4．定积分${∫}_{0}^{1}$（2x+ex）dx的值为（ ）
| A． | e+2 | B． | e+1 | C． | e | D． | e-1 |
11．圆ρ=2$\sqrt{2}$（cosθ-sinθ）的圆心极坐标是（ ）
| A． | $（\sqrt{2}，\frac{3π}{4}）$ | B． | $（{2，\frac{7π}{4}}）$ | C． | $（2，\frac{5π}{4}）$ | D． | $（{2，\frac{3π}{4}}）$ |
8．
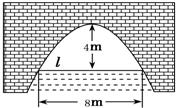如图是抛物线形拱桥，当水面在l时，拱顶离水面4米，水面宽8米．水位上升1米后，水面宽为（ ）
如图是抛物线形拱桥，当水面在l时，拱顶离水面4米，水面宽8米．水位上升1米后，水面宽为（ ）| A． | $\sqrt{3}$米 | B． | $2\sqrt{3}$米 | C． | $3\sqrt{3}$米 | D． | $4\sqrt{3}$米 |