题目内容
11.圆ρ=2$\sqrt{2}$(cosθ-sinθ)的圆心极坐标是( )| A. | $(\sqrt{2},\frac{3π}{4})$ | B. | $({2,\frac{7π}{4}})$ | C. | $(2,\frac{5π}{4})$ | D. | $({2,\frac{3π}{4}})$ |
分析 把圆的极坐标方程化为直角坐标方程,经过配方可得圆心直角坐标,再化为极坐标即可得出.
解答 解:圆ρ=2$\sqrt{2}$(cosθ-sinθ)即:ρ2=2$\sqrt{2}$ρ(cosθ-sinθ),
化为直角坐标方程:x2+y2=2$\sqrt{2}$(x-y),
配方为:$(x-\sqrt{2})^{2}$+$(y+\sqrt{2})^{2}$=4.
圆心C$(\sqrt{2},-\sqrt{2})$,可得极坐标$ρ=\sqrt{(\sqrt{2})^{2}+(-\sqrt{2})^{2}}$=2,tanθ=$\frac{-\sqrt{2}}{\sqrt{2}}$-1,且θ在第四象限,
∴θ=$\frac{7π}{4}$.
∴圆心C极坐标为$(2,\frac{7π}{4})$.
故选:B.
点评 本题考查了极坐标方程与直角坐标方程的互化、圆的标准方程,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
1.若函数f(x)为定义在R上的偶函数,其导函数为f′(x),对任意实数x满足xf′(x)>-f(-x),则不等式xf(x)<(1-2x)f(1-2x)的解集是( )
| A. | (0,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,+∞) | C. | (-∞,$\frac{1}{3}$) | D. | (-∞,$\frac{1}{3}$)∪($\frac{1}{3}$,+∞) |
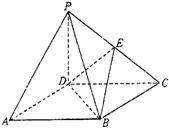 如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.