题目内容
(本小题满分13分)
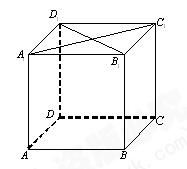
 如图,已知四棱柱ABCD—A1B1C1D1的底面是菱形,侧棱BB1⊥底面ABCD,E是侧棱CC1的中点。
如图,已知四棱柱ABCD—A1B1C1D1的底面是菱形,侧棱BB1⊥底面ABCD,E是侧棱CC1的中点。
(I)求证:AC⊥平面BDD1B1;
(II)求证:AC//平面B1DE。
 如图,已知四棱柱ABCD—A1B1C1D1的底面是菱形,侧棱BB1⊥底面ABCD,E是侧棱CC1的中点。
如图,已知四棱柱ABCD—A1B1C1D1的底面是菱形,侧棱BB1⊥底面ABCD,E是侧棱CC1的中点。
(I)求证:AC⊥平面BDD1B1;
(II)求证:AC//平面B1DE。
证明:(I)因为ABCD为菱形,所以

因为BB1⊥底面ABCD,
所以BB1⊥AC。 …………3分
所以AC⊥平面BDD1B1。 …………5分
(II)设AC,BD交于点O,取B1D的中点F,连结OF,EF,

则OF//BB1,且
又E是侧棱CC1的中点,

所以OF//CC1,且OF= , ………………7分
, ………………7分
所以四边形OCEF为平行四边形,OC//EF, ………………9分
又A C
C 平面B1DE,EF
平面B1DE,EF 平面B1DE, ………………11分
平面B1DE, ………………11分
所以AC//平面B1DE。………………13分

因为BB1⊥底面ABCD,
所以BB1⊥AC。 …………3分
所以AC⊥平面BDD1B1。 …………5分
(II)设AC,BD交于点O,取B1D的中点F,连结OF,EF,

则OF//BB1,且

又E是侧棱CC1的中点,

所以OF//CC1,且OF=
 , ………………7分
, ………………7分所以四边形OCEF为平行四边形,OC//EF, ………………9分
又A
 C
C 平面B1DE,EF
平面B1DE,EF 平面B1DE, ………………11分
平面B1DE, ………………11分所以AC//平面B1DE。………………13分

练习册系列答案
相关题目
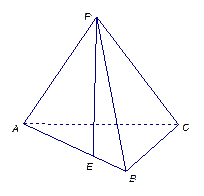
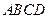 中,
中, 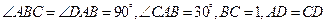 ,
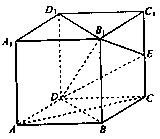
,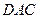 沿对角线
沿对角线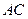 折起后如图2所示(点
折起后如图2所示(点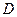 记为点
记为点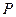 ), 点
), 点 上的正投影
上的正投影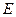 落在线段
落在线段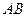 上, 连接
上, 连接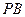 .
.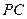 与平面
与平面 所成的角的大小;
所成的角的大小; 的大小的余弦值.
的大小的余弦值.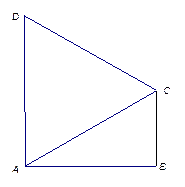
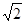 a,侧棱AA1=2a,点D是AA1的中点,那么截面DBC与底面ABC所成二面角的大小是________.
a,侧棱AA1=2a,点D是AA1的中点,那么截面DBC与底面ABC所成二面角的大小是________. 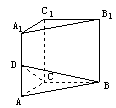
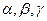 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: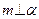 ,
,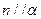 ,则
,则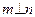 ②若
②若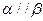 ,
,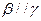 ,
,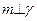
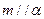 ,
,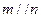 ④若
④若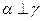 ,
,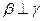 ,则
,则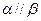
 中,
中, ,
, ,则
,则 的长为 ( )
的长为 ( )


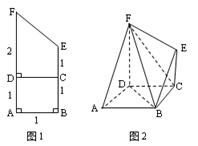
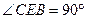 时,二面角C—EF—B的平面角的余弦值等于 。
时,二面角C—EF—B的平面角的余弦值等于 。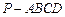 的三视图如图
的三视图如图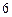 所示,则四棱锥
所示,则四棱锥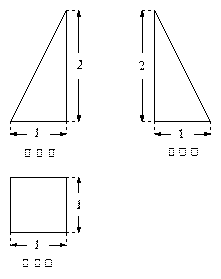
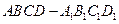 中,
中,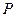 是侧棱
是侧棱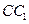 上的一点,
上的一点,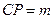 .
.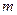 ,使直线
,使直线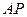 与平面
与平面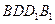
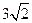 ;
;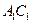 上是否存在一个定点
上是否存在一个定点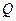 ,
,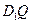 在平面
在平面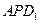 上
上