题目内容
(本小题满分12分)
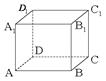
将如图1的直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连结EB、FB、FA后围成一个空间几何体如图2所示,
(1)求异面直线BD与EF所成角的大小;
(2)求二面角D—BF—E的大小;
(3)求这个几何体的体积.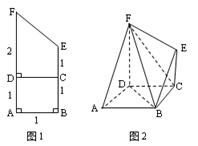
将如图1的直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连结EB、FB、FA后围成一个空间几何体如图2所示,
(1)求异面直线BD与EF所成角的大小;
(2)求二面角D—BF—E的大小;
(3)求这个几何体的体积.

(1) (2)
(2) (3)
(3)
 (2)
(2) (3)
(3)
解法一:(1)将图形补充成长方体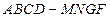 ,
,
连 ,则
,则
 ,又连
,又连 ,易知
,易知
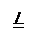 ∴
∴ ,∴
,∴ 与
与 所成角为
所成角为 ………… 4分
………… 4分
(2)取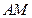 的中点
的中点 ,连
,连 ,则
,则
 ,而
,而 平面
平面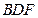
∴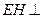 平面
平面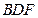 ,又
,又 过
过 的中点,即
的中点,即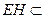 平面
平面
∴平面 平面
平面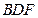
∴二面角 —
— —
— 的大小为
的大小为 ………… 8分
………… 8分
(3)

 ………… 12分
………… 12分
 解法二:建立空间直角坐标系(如图)
解法二:建立空间直角坐标系(如图)
(1) ,
,

∴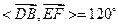
∴异面直线 与
与 所成角为
所成角为 ………… 4分
………… 4分
(2)显然平面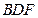 的一个法向量为
的一个法向量为
设平面 的一个法向量为
的一个法向量为
又
 由
由 ,
,
得 取
取 得
得
而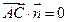 ∴平面
∴平面 平面
平面
∴二面角 —
— —
— 的大小为
的大小为 ………… 8分
………… 8分
(3)同解法(1) ………… 12分
 ,
,连
 ,则
,则
 ,又连
,又连 ,易知
,易知
 ∴
∴ ,∴
,∴ 与
与 所成角为
所成角为 ………… 4分
………… 4分
(2)取
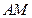 的中点
的中点 ,连
,连 ,则
,则
 ,而
,而 平面
平面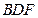
∴
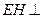 平面
平面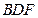 ,又
,又 过
过 的中点,即
的中点,即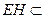 平面
平面
∴平面
 平面
平面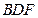
∴二面角
 —
— —
— 的大小为
的大小为 ………… 8分
………… 8分(3)


 ………… 12分
………… 12分 解法二:建立空间直角坐标系(如图)
解法二:建立空间直角坐标系(如图)(1)
 ,
,

∴
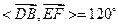
∴异面直线
 与
与 所成角为
所成角为 ………… 4分
………… 4分(2)显然平面
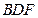 的一个法向量为
的一个法向量为
设平面
 的一个法向量为
的一个法向量为
又

 由
由 ,
,
得
 取
取 得
得
而
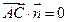 ∴平面
∴平面 平面
平面
∴二面角
 —
— —
— 的大小为
的大小为 ………… 8分
………… 8分(3)同解法(1) ………… 12分

练习册系列答案
相关题目
 ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.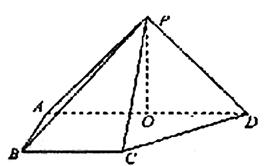
 中,
中, 、
、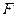 分别为棱
分别为棱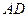 、
、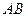 的中点.
的中点.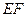 ∥平面
∥平面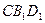 ;
;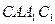 ⊥平面
⊥平面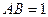 ,一个动点从点
,一个动点从点 、
、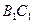 、
、 、
、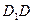 、
、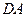 上的点,最终又回到点
上的点,最终又回到点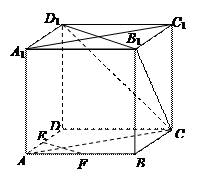
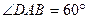 ,AB=AD=2CD,侧面
,AB=AD=2CD,侧面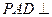 底面ABCD,且
底面ABCD,且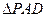 为等腰直角三角形,
为等腰直角三角形,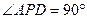 ,M为AP的中点。
,M为AP的中点。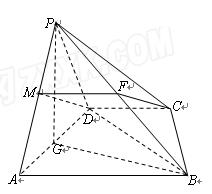
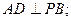
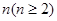 条直线,其中任意两条不平行,任意三条不共点。
条直线,其中任意两条不平行,任意三条不共点。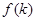 表示
表示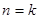 时平面被分成的区域数,则
时平面被分成的区域数,则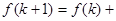 ( )
( )



 如图,已知四棱柱ABCD—A1B1C1D1的底面是菱形,侧棱BB1⊥底面ABCD,E是侧棱CC1的中点。
如图,已知四棱柱ABCD—A1B1C1D1的底面是菱形,侧棱BB1⊥底面ABCD,E是侧棱CC1的中点。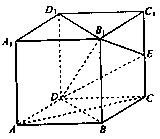
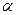 、
、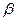 、
、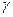 两两互相垂直,长为
两两互相垂直,长为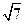 的线段AB在
的线段AB在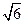 、a、b,则
、a、b,则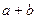 的最大值为 。
的最大值为 。