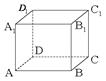
题目内容
如图1,在直角梯形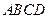 中,
中, 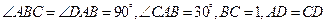 ,
,
把△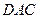 沿对角线
沿对角线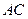 折起后如图2所示(点
折起后如图2所示(点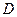 记为点
记为点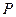 ), 点
), 点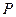 在平面
在平面 上的正投影
上的正投影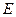 落在线段
落在线段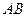 上, 连接
上, 连接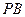 .
.
(1) 求直线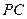 与平面
与平面 所成的角的大小;
所成的角的大小;
(2) 求二面角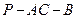 的大小的余弦值.
的大小的余弦值.
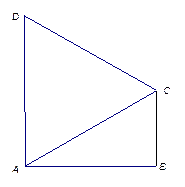
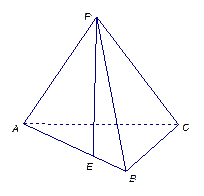
图1 图2
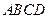 中,
中, 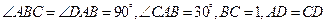 ,
,把△
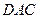 沿对角线
沿对角线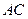 折起后如图2所示(点
折起后如图2所示(点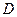 记为点
记为点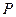 ), 点
), 点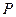 在平面
在平面 上的正投影
上的正投影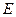 落在线段
落在线段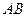 上, 连接
上, 连接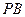 .
.(1) 求直线
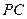 与平面
与平面 所成的角的大小;
所成的角的大小;(2) 求二面角
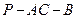 的大小的余弦值.
的大小的余弦值.

图1 图2
(1) (2)
(2)
 (2)
(2)
(1) 解:在图4中,
∵
∴ ,
,  ,
,  .
.
∵ ,
,
∴△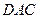 为等边三角形.
为等边三角形.
∴ . …2分
. …2分
在图5中,
∵点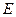 为点
为点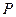 在平面
在平面 上的正投影,
上的正投影,
∴ 平面
平面 .
.
∵ 平面
平面 ,
,
∴
 .
.
∵ ,
,
∴ .
.
∵ 平面
平面 ,
,  平面
平面 ,
,
∴ 平面
平面 .
.
∴ 为直线
为直线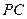 与平面
与平面 所成的角. …4分
所成的角. …4分
在Rt△ 中,
中,  ,
,
∴ .
.
∵ ,
,
∴ .
.
∴直线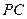 与平面
与平面 所成的角为
所成的角为 . …6分
. …6分
(2) 解:取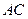 的中点
的中点 , 连接
, 连接 ,
, .
.
∵ ,
,
∴ .
.
∵ 平面
平面 ,
, 平面
平面 ,
,
∴ .
.
∵ 平面
平面 ,
,  平面
平面 ,
,
∴ 平面
平面 .
.
∵ 平面
平面 ,
,
∴ .
.
∴ 为二面角
为二面角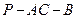 的平面角. …8分
的平面角. …8分
在Rt△ 中,
中, ,
,
∴

 ,
, .
.
在Rt△ 中,
中, .
.
在Rt△ 中,
中, .
.
∴二面角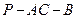 的大小的余弦值为
的大小的余弦值为 . …12分
. …12分
方法二:
解:在图4中,
∵

∴ ,
,  ,
,  .
.
∵ ,
,
∴△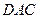 为等边三角形.
为等边三角形.
∴ . …2分
. …2分
在图5中,
∵点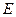 为点
为点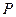 在平面
在平面 上的射影, 图4
上的射影, 图4

∴ 平面
平面 .
.
∵ 平面
平面 ,
,
∴
 .
.
∵ ,
,
∴ .
.
∵ 平面
平面 ,
,  平面
平面 ,
,
∴ 平面
平面 . …4分
. …4分
连接 ,
,
在Rt△ 和Rt△
和Rt△ 中,
中, ,
,
∴Rt△
 Rt△
Rt△ .
.
∴ .
.
∴ .
.
∴ .
.
在Rt△ 中,
中, .
.
∴ .
.
在Rt△ 中,
中,
 . …6分
. …6分
以点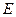 为原点,
为原点, 所在直线为
所在直线为 轴,与
轴,与 平行的直线为
平行的直线为 轴,
轴, 所在直线为
所在直线为 轴,建立空
轴,建立空
间直角坐标系 ,则
,则 ,
, ,
, ,
, ,
,
 .
.
∴ ,
, ,
, ,
, .
.
(1)∵
 ,
,
∴ .
.
∴直线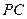 与平面
与平面 所成的角为
所成的角为 . …9分
. …9分
(2) 设平面 的法向量为n
的法向量为n ,
,
由 得
得
令 , 得
, 得 ,
, .
.
∴n 为平面
为平面 的一个法向量.
的一个法向量.
∵ 为平面
为平面 的一个法向量,
的一个法向量,
∴


 .
.
∵二面角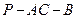 的平面角为锐角,
的平面角为锐角,
∴二面角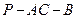 的平面角的余弦值为
的平面角的余弦值为 . …12分
. …12分
∵

∴
 ,
,  ,
,  .
.∵
 ,
,∴△
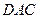 为等边三角形.
为等边三角形. ∴
 . …2分
. …2分在图5中,
∵点
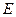 为点
为点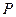 在平面
在平面 上的正投影,
上的正投影,∴
 平面
平面 .
.∵
 平面
平面 ,
,∴

 .
.∵
 ,
, ∴
 .
.∵
 平面
平面 ,
,  平面
平面 ,
,∴
 平面
平面 .
.∴
 为直线
为直线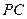 与平面
与平面 所成的角. …4分
所成的角. …4分在Rt△
 中,
中,  ,
,∴
 .
. ∵
 ,
,∴
 .
.∴直线
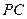 与平面
与平面 所成的角为
所成的角为 . …6分
. …6分 (2) 解:取
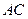 的中点
的中点 , 连接
, 连接 ,
, .
.∵
 ,
,∴
 .
.∵
 平面
平面 ,
, 平面
平面 ,
,∴
 .
.∵
 平面
平面 ,
,  平面
平面 ,
,∴
 平面
平面 .
.∵
 平面
平面 ,
,∴
 .
.∴
 为二面角
为二面角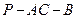 的平面角. …8分
的平面角. …8分在Rt△
 中,
中, ,
,∴


 ,
, .
.在Rt△
 中,
中, .
. 在Rt△
 中,
中, .
.∴二面角
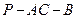 的大小的余弦值为
的大小的余弦值为 . …12分
. …12分方法二:
解:在图4中,
∵


∴
 ,
,  ,
,  .
.∵
 ,
,∴△
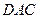 为等边三角形.
为等边三角形. ∴
 . …2分
. …2分在图5中,
∵点
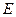 为点
为点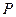 在平面
在平面 上的射影, 图4
上的射影, 图4
∴
 平面
平面 .
.∵
 平面
平面 ,
,∴

 .
.∵
 ,
, ∴
 .
.∵
 平面
平面 ,
,  平面
平面 ,
, ∴
 平面
平面 . …4分
. …4分连接
 ,
,在Rt△
 和Rt△
和Rt△ 中,
中, ,
,∴Rt△

 Rt△
Rt△ .
.∴
 .
.∴
 .
.∴
 .
.在Rt△
 中,
中, .
.∴
 .
.在Rt△
 中,
中,
 . …6分
. …6分以点
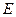 为原点,
为原点, 所在直线为
所在直线为 轴,与
轴,与 平行的直线为
平行的直线为 轴,
轴, 所在直线为
所在直线为 轴,建立空
轴,建立空 间直角坐标系
 ,则
,则 ,
, ,
, ,
, ,
, .
.∴
 ,
, ,
, ,
, .
. (1)∵

 ,
,∴
 .
.∴直线
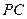 与平面
与平面 所成的角为
所成的角为 . …9分
. …9分 (2) 设平面
 的法向量为n
的法向量为n ,
,由
 得
得
令
 , 得
, 得 ,
, .
.∴n
 为平面
为平面 的一个法向量.
的一个法向量. ∵
 为平面
为平面 的一个法向量,
的一个法向量,∴



 .
.∵二面角
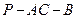 的平面角为锐角,
的平面角为锐角,∴二面角
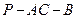 的平面角的余弦值为
的平面角的余弦值为 . …12分
. …12分
练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
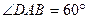 ,AB=AD=2CD,侧面
,AB=AD=2CD,侧面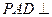 底面ABCD,且
底面ABCD,且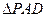 为等腰直角三角形,
为等腰直角三角形,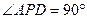 ,M为AP的中点。
,M为AP的中点。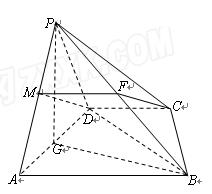
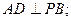
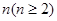 条直线,其中任意两条不平行,任意三条不共点。
条直线,其中任意两条不平行,任意三条不共点。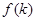 表示
表示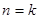 时平面被分成的区域数,则
时平面被分成的区域数,则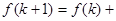 ( )
( )



 如图,已知四棱柱ABCD—A1B1C1D1的底面是菱形,侧棱BB1⊥底面ABCD,E是侧棱CC1的中点。
如图,已知四棱柱ABCD—A1B1C1D1的底面是菱形,侧棱BB1⊥底面ABCD,E是侧棱CC1的中点。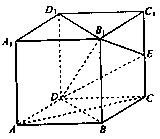
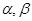 和直线,给出条件:①
和直线,给出条件:①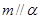 ;②
;②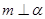 ;③
;③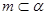 ;④
;④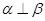 ;⑤
;⑤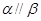 .则当满足条件 时,有
.则当满足条件 时,有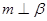 成立;(填所选条件的序号)
成立;(填所选条件的序号)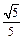
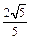
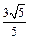
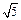
 ( )
( )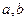 和平面
和平面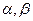 .给定下列四个命题:
.给定下列四个命题: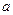 ∥
∥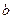 ,
,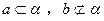 ,那么
,那么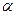 ;
;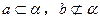 ,且
,且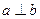 ,则
,则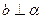 ;
;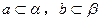 ,且
,且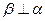 ;
;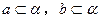 ,且
,且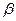 ,
,