题目内容
2.已知函数f(x)是定义在R上的偶函数,且当x≥0时,f(x)=x|x-2|.若关于x的方程f2(x)+af(x)+b=0(a,b∈R)恰有10个不同实数解,则a的取值范围为( )| A. | (0,2) | B. | (-2,0) | C. | (1,2) | D. | (-2,-1) |
分析 根据函数的奇偶性求出f(x)的解析式,令t=f(x),将方程转化为一元二次函数,由根与系数之间的关系进行求解即可.
解答 解:设x<0,则-x>0,满足表达式f(x)=x|x-2|.
∴f(-x)=-x|-x-2|=-x|x+2|,
又∵f(x)为偶函数,∴f(-x)=f(x),
∴f(x)=-x|x+2|,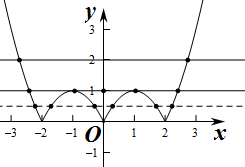
故当x<0时,f(x)=-x|x+2|.
则f(x)=$\left\{\begin{array}{l}{x|x-2|,x≥0}\\{-x|x+2|,x<0}\end{array}\right.$,
作出f(x)的图象如图:
设t=f(x),
由图象知,当t>1时,t=f(x)有两个根,
当t=1时,t=f(x)有四个根,
当0<t<1时,t=f(x)有六两个根,
当t=0时,t=f(x)有三个根,
当t<0时,t=f(x)有0个根,
则方程[f(x)]2+af(x)+b=0等价为t2+at+b=0,
若方程[f(x)]2+af(x)+b=0(a∈R)恰好有1个不同实数解,
等价为方程t2+at+b=0有两不同的根,
且0<t1<1,t2=1,
则t1+t2=-a,
即1<t1+t2<2,
则1<-a<2,
即-2<a<-1,
则a的取值范围为(-2,-1),
故选D.
点评 本题考查函数的单调性和奇偶性的运用,主要考查方程与函数的零点的关系,利用换元法转化为一元二次方程根与系数之间的关系是解决本题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
13.九江气象台统计,5月1日浔阳区下雨的概率为$\frac{4}{15}$,刮风的概率为$\frac{2}{15}$,既刮风又下雨的概率为$\frac{1}{10}$,设A为下雨,B为刮风,那么P(A|B)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{8}$ |
7.集合A={x|x2-3x+2=0},B={0,1},则A∪B=( )
| A. | {1} | B. | {0,1,2} | C. | (1,2) | D. | (-1,2] |
11.已知函数f(x)=x2+tx+t,?x∈R,f(x)>0,函数g(x)=3x2-2(t+1)x+t,则“?a,b∈(0,1)使得g(a)=g(b)=0”为真命题的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
12.已知x与y之间的一组数据:
已求得关于y与x的线性回归方程$\stackrel{∧}{y}$=1.2x+0.55,则a的值为2.15.
| x | 0 | 2 | 4 | 6 |
| y | a | 3 | 5 | 3a |
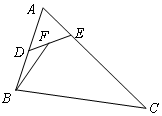 如图,在△ABC中,已知AB=2,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=5$\overrightarrow{AE}$,
如图,在△ABC中,已知AB=2,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=5$\overrightarrow{AE}$,