题目内容
已知函数 .
.
(Ⅰ)当 时,求
时,求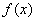 在区间
在区间 上的最值;
上的最值;
(Ⅱ)讨论函数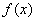 的单调性;
的单调性;
(Ⅲ)当 时,有
时,有 恒成立,求
恒成立,求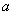 的取值范围.
的取值范围.
解析:(Ⅰ)当 时,
时, ,
,
∴ .
.
∵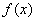 的定义域为
的定义域为 ,∴由
,∴由 得
得 .
.
∴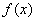 在区间
在区间 上的最值只可能在
上的最值只可能在 取到,
取到,
而 ,
,
∴ .
.
(Ⅱ) .
.
①当 ,即
,即 时,
时, 在
在 单调递减;
单调递减;
②当 时,
时, 在
在 单调递增;
单调递增;
③当 时,由
时,由 得
得 或
或 (舍去)
(舍去)
∴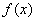 在
在 单调递增,在
单调递增,在 上单调递减;
上单调递减;
综上,当 时,
时,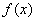 在
在 单调递增;
单调递增;
当 时,
时,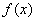 在
在 单调递增,在
单调递增,在 上单调递减;
上单调递减;
当 时,
时,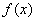 在
在 单调递减.
单调递减.
(Ⅲ)由(Ⅱ)知,当 时,
时,
即原不等式等价于
即
整理得 ∴
∴ ,
,
又∵ ,所以
,所以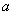 的取值范围为
的取值范围为 .
.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 满足
满足 ,则下列关系式恒成立的是( )
,则下列关系式恒成立的是( ) B.
B.  C.
C.  D.
D. 
 -
- =1(a>0,b>0)的离心率为e=2,过双曲线上一点M作直线MA,MB交双曲线于A,B两点
=1(a>0,b>0)的离心率为e=2,过双曲线上一点M作直线MA,MB交双曲线于A,B两点 ,且斜率分别为k1,k2,若直线AB过原点O,则k1·k2的值为________.
,且斜率分别为k1,k2,若直线AB过原点O,则k1·k2的值为________.
 的定义域为 ( )
的定义域为 ( ) B.
B.  C.
C.  D.
D. 
 的大致图象为( )
的大致图象为( )
 .
. ,使得对任意的
,使得对任意的 ,当
,当 时恒有
时恒有 成立.若存在,求
成立.若存在,求 列式运算
列式运算 =a1a4-a2a3.将函数f(x)=
=a1a4-a2a3.将函数f(x)= 的图象向左平移
的图象向左平移 个单位,以下是所得函数图象的一个对称中心是
个单位,以下是所得函数图象的一个对称中心是 ( )
( ) B.
B.  C.
C.  D.
D. 

 =____________.
=____________.