题目内容
1.设随机变量?服从?~N(2,9),若P(?>c+1)=P(?<c-1),则c=( )| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
分析 画正态曲线图,由对称性得c-1与c+1的中点是2,由中点坐标公式得到c的值.
解答  解:∵N(2,32),
解:∵N(2,32),
∴P(ξ>c+1)=1-P(ξ≤c+1)=Φ($\frac{c+1-2}{3}$),
P(ξ<c-1)=Φ($\frac{c-1-2}{3}$),
∴Φ($\frac{c-3}{3}$)+Φ($\frac{c-1}{3}$)=1,
∴1-Φ($\frac{3-c}{3}$)+Φ($\frac{c-1}{3}$)=1,
解得c=2,
故选:D.
点评 本题考查正态分布,正态曲线有两个特点:(1)正态曲线关于直线x=μ对称;(2)在正态曲线下方和x轴上方范围内的区域面积为为1.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
13.函数y=$\sqrt{3}$sin2x+cos2x的最小正周期为( )
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | π | D. | 2π |
11.在正方体ABCD-A1B1C1D1中,E为棱CD的中点,则( )
| A. | A1E⊥DC1 | B. | A1E⊥BD | C. | A1E⊥BC1 | D. | A1E⊥AC |
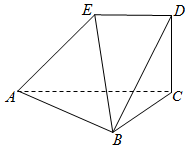 如图,AC=2ED,AC∥平面EDB,AC⊥平面BCD,平面ACDE⊥平面ABC.
如图,AC=2ED,AC∥平面EDB,AC⊥平面BCD,平面ACDE⊥平面ABC.