题目内容
集合{1,2,3}的真子集的个数有( )
| A、8个 | B、7个 |
| C、6 个 | D、5个 |
考点:子集与真子集
专题:集合
分析:根据集合的子集的个数运算规律得出合{1,2,3}的子集有23=8个,
再根据真子集的概念判断集合{1,2,3}是集合{1,2,3}的子集,不是真子集,从而得出答案.
再根据真子集的概念判断集合{1,2,3}是集合{1,2,3}的子集,不是真子集,从而得出答案.
解答:
解:∵集合{1,2,3}的子集有23=8个,
集合{1,2,3}是集合{1,2,3}的子集,不是真子集,
∴集合{1,2,3}的真子集的个数有7个,
故选:B
集合{1,2,3}是集合{1,2,3}的子集,不是真子集,
∴集合{1,2,3}的真子集的个数有7个,
故选:B
点评:本题简单的考察了集合的子集真子集的概念,属于容易题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|≤
,x∈R)的部分图象如图所示,则该函数表达式为( )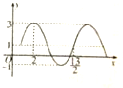
| π |
| 6 |

A、y=2sin(
| ||||
B、y=2sin(
| ||||
C、y=2sin(
| ||||
D、y=2sin(
|
等比数列{an}中,a4=4,则a2•a6等于( )
| A、4 | B、8 | C、16 | D、32 |
函数y=
的定义域为( )
| 1-lnx |
| A、(0,e] |
| B、(-∞,e] |
| C、(0,10] |
| D、(-∞,10] |
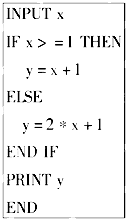 读程序,完成下列题目:程序如图:
读程序,完成下列题目:程序如图: