题目内容
19.已知xe-f(x)=1-e-x,0<x<m,求证f(x)<$\frac{m}{2}$.分析 通过分析只需证明$\frac{1}{x}$(1-e-x)>${e}^{-\frac{x}{2}}$成立即可,通过记g(x)=1-e-x-x•${e}^{-\frac{x}{2}}$、求导可知g′(x)=${e}^{-\frac{x}{2}}$(${e}^{-\frac{x}{2}}$-1+$\frac{x}{2}$),再通过对h(x)=${e}^{-\frac{x}{2}}$-1+$\frac{x}{2}$求导、计算可知h(x)>h(0)=0,进而可知函数g(x)单调递增,从而1-e-x-x•${e}^{-\frac{x}{2}}$>0,进而证明了$\frac{1}{x}$(1-e-x)>${e}^{-\frac{x}{2}}$,利用指数函数的单调性即得结论.
解答 证明:∵xe-f(x)=1-e-x,
∴e-f(x)=$\frac{1}{x}$(1-e-x),
故只需证:$\frac{1}{x}$(1-e-x)>${e}^{-\frac{x}{2}}$,
记g(x)=1-e-x-x•${e}^{-\frac{x}{2}}$,则g′(x)=e-x-${e}^{-\frac{x}{2}}$+$\frac{x}{2}$•${e}^{-\frac{x}{2}}$=${e}^{-\frac{x}{2}}$(${e}^{-\frac{x}{2}}$-1+$\frac{x}{2}$),
记h(x)=${e}^{-\frac{x}{2}}$-1+$\frac{x}{2}$,则h′(x)=-$\frac{1}{2}$•${e}^{-\frac{x}{2}}$+$\frac{1}{2}$>0,
∴h(x)>h(0)=0,
∴g′(x)>0,即函数g(x)单调递增,
∴g(x)=1-e-x-x•${e}^{-\frac{x}{2}}$>g(0)=0,
∴$\frac{1}{x}$(1-e-x)>${e}^{-\frac{x}{2}}$,
从而e-f(x)>${e}^{-\frac{x}{2}}$,
∴-f(x)>-$\frac{x}{2}$,f(x)<$\frac{x}{2}$,
又∵0<x<m,
∴f(x)<$\frac{x}{2}$<$\frac{m}{2}$.
点评 本题考查借助函数的单调性证明不等式,考查运算求解能力,注意解题方法的积累,属于中档题.

 小学教材完全解读系列答案
小学教材完全解读系列答案| A. | 4x2+y2=1 | B. | x2+4y2=1 | C. | $\frac{{x}^{2}}{4}$+y2=1 | D. | x2$+\frac{{y}^{2}}{4}$=1 |
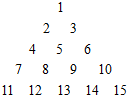 把自然数1,2,3,4,…按如图方法排成一个数阵,根据如图排列规律,求数列中第n(n≥3)行从左到右的第三个数.
把自然数1,2,3,4,…按如图方法排成一个数阵,根据如图排列规律,求数列中第n(n≥3)行从左到右的第三个数.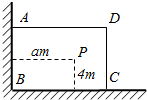 如图,有-直角墙角,两边的长度足够长,在P处有-棵树与两墙的距离分别是a米(0<a<12),4米,不考虑树的粗细,现在想用16米长的篱笆,借助墙角围成-个矩形的花围ABCD,并要求将这棵树围在花圃内或在花圃的边界上.设BC=x米,此矩形花围的面积为y平方米.
如图,有-直角墙角,两边的长度足够长,在P处有-棵树与两墙的距离分别是a米(0<a<12),4米,不考虑树的粗细,现在想用16米长的篱笆,借助墙角围成-个矩形的花围ABCD,并要求将这棵树围在花圃内或在花圃的边界上.设BC=x米,此矩形花围的面积为y平方米.